练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

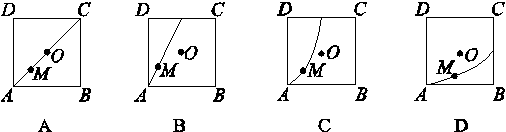
    如图，正三角形PAD所在平面与正方形ABCD所在平面互相垂直，O为正方形ABCD的中心，M为正方形ABCD内一点，且满足MP＝MB，则点M的轨迹为(　　)


    B　命题立意：本题考查空间直线与平面的位置关系和空间想象能力，难度中等．

    解题思路：利用平面的基本性质求解．由MP＝MB得点P在线段PB的垂直平分面上，又点M在平面ABCD上，所以点M在两个平面的交线上，而两个平面的交线是一条直线．又OB≠OP，所以交线不经过点O，故选B.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    现要从20名学生中抽取5名进行问卷调查，请按正确的顺序表示抽取样本的过程：________(填序号)．

    ① 编号：将20名学生按1到20进行编号；

    ② 装箱：将号签放在同一箱中，并搅拌均匀；

    ③ 抽签：从箱中依次抽出5个号签；

    ④ 制签：将1到20这20个号码写在形状、大小完全相同的号签上；

    ⑤ 取样：将与号签号码相同的5个学生取出．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A＝{x||x－1|＜2}，B＝{x|log2x＜2}，则A∩B＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    命题p：∃x∈R，使；命题q：∀x∈(0，＋∞)，x2－2ax＋1≥0.若命题p∧q为真，则实数a的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，AB＝2，BC＝1.5，∠ABC＝120°(如图所示)，若将△ABC绕BC边所在直线旋转一周，则所形成的旋转体的体积是(　　)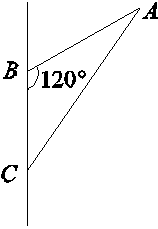

    A.π                                  B.π

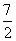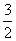    C.π                                  D.π

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正方体ABCD－A1B1C1D1的棱长为1，则以正方体ABCD－A1B1C1D1的中心为顶点，以平面AB1D1截正方体外接球所得的圆为底面的圆锥的表面积为______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在矩形ABCD中，AB＝4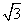，BC＝2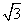，且矩形ABCD的顶点都在半径为R的球O的球面上，若四棱锥O－ABCD的体积为8，则球O的半径R＝(　　)

    A．3                                    B.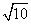 

    C．2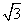                                 D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列{an}的前n项和为Sn，且Sn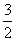＝(an－1)，数列{bn}满足bn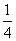＝bn－1－(n≥2)，且b1＝3.

    (1)求数列{an}与{bn}的通项公式；

    (2)设数列{cn}满足cn＝an·log2(bn＋1)，其前n项和为Tn，求Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    　已知复数z1满足(z1－2)(1＋i)＝1－i(i为虚数单位)，复数z2的虚部为2，且z1·z2是实数，求z2.

    查看答案和解析>>

    同步练习册答案