练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知正方体ABCD－A1B1C1D1的棱长为1，则以正方体ABCD－A1B1C1D1的中心为顶点，以平面AB1D1截正方体外接球所得的圆为底面的圆锥的表面积为______．


    π　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某学校高一、高二、高三年级的学生人数之比为3∶3∶4，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本，则应从高二年级抽取________名学生．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知R是实数集，集合A＝{y|y＝x2－2x＋2，x∈R，－1≤x≤2}，集合B＝，任取x∈A，则x∈A∩B的概率等于________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示是一个几何体的三视图，其侧(左)视图是一个边长为a的等边三角形，俯视图是两个正三角形拼成的菱形，则该几何体的体积为(　　)

    A．a3　　 B.    C.   D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


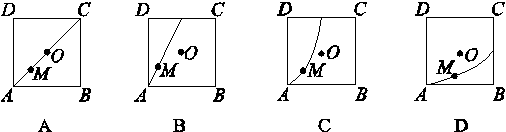
    如图，正三角形PAD所在平面与正方形ABCD所在平面互相垂直，O为正方形ABCD的中心，M为正方形ABCD内一点，且满足MP＝MB，则点M的轨迹为(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在三棱锥A－BCD中，侧棱AB，AC，AD两两垂直，△ABC，△ACD，△ADB的面积分别为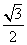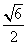，，，则该三棱锥外接球的表面积为(　　)

    A．2π                                  B．6π 

    C．4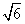π                              D．24π

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在三棱锥O－ABC中，三条棱OA，OB，OC两两垂直，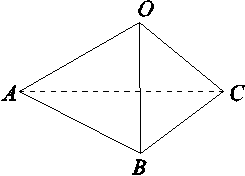

    且OA＞OB＞OC，分别经过三条棱OA，OB，OC作一个截面平分三棱锥的体积，截面面积依次为S1，S2，S3，则S1，S2，S3的大小关系为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数y＝Asin(ωx＋φ)＋k(A＞0)的最大值为4，最小值为0，最小正周期为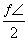，直线x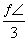＝是其图象的一条对称轴，则下面各式中符合条件的解析式为(　　)

    A．y＝4sin　 　                 B．y＝2sin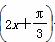＋2

    C．y＝2sin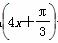＋2                   D．y＝2sin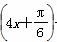＋2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若复数z＝1＋i(i为虚数单位)，是z的共轭复数，则z2＋2的虚部为________．

    查看答案和解析>>

    同步练习册答案