
| A. | f(x)=x3-x2+x | B. | f(x)=-2x+sinx | C. | f(x)=ex-e-x | D. | f(x)=1+xlnx |
分析 若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则函数y=f(x)的导函数上存在两点,使这点的导函数值乘积为-1,进而可得答案.
解答 解:函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,
则函数y=f(x)的导函数上存在两点,使这点的导函数值乘积为-1,
当f(x)=x3-x2+x时,f′(x)=3x2-2x+1≥$\frac{2}{3}$,不满足条件;
当f(x)=-2x+sinx时,f′(x)=-2+cosx<0恒成立,不满足条件;
当f(x)=ex-e-x时,f′(x)=ex+e-x≥2,不满足条件;
当f(x)=1+xlnx时,f′(x)=1+lnx∈R,满足条件.
故选:D.
点评 本题考查的知识点是利用导数研究曲线上某点切线方程,转化思想,难度中档.


科目:高中数学 来源: 题型:选择题
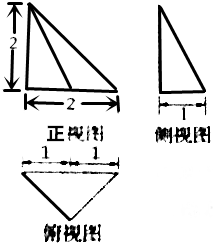
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k<-1 | B. | k≤-1 | C. | k>-1 | D. | k≥-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
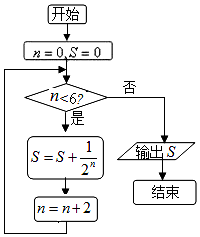
| A. | $\frac{5}{4}$ | B. | $\frac{21}{16}$ | C. | $\frac{63}{32}$ | D. | $\frac{85}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com