考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)f′(x)=
;讨论导数的正负以确定单调性,从而求最小值,从而求a;
(2)f(x)<x
2在(1,+∞)上恒成立可化为a>xlnx-x
3在(1,+∞)上恒成立;令F(x)=xlnx-x
3,从而化为函数的最值问题.
解答:
解:(1)f′(x)=
;
①当-1≤a<0时,f(x)在[1,e]上是增函数,
故f(1)=0-a=
,故a=-
(舍去);
②当-e<a<-1时,f(x)在[1,e]上先减后增,
故f(-a)=ln(-a)+1=
,故a=-
;
③当a≤-e时,f(x)在[1,e]上是减函数,
故f(e)=1-
=
,故a=-
(舍去);
故a=-
;
(2)f(x)<x
2在(1,+∞)上恒成立可化为
a>xlnx-x
3在(1,+∞)上恒成立;
令F(x)=xlnx-x
3,
则F′(x)=lnx+1-3x
2,
F″(x)=
-6x;
当x≥1时,F″(x)<0;
故F′(x)=lnx+1-3x
2在(1,+∞)上是减函数,
故F′(x)<F′(1)=0+1-3<0;
故F(x)=xlnx-x
3在(1,+∞)上是减函数,
故F(x)<0-1=-1;
故a≥-1.
点评:本题考查了导数的综合应用及恒成立问题,属于中档题.



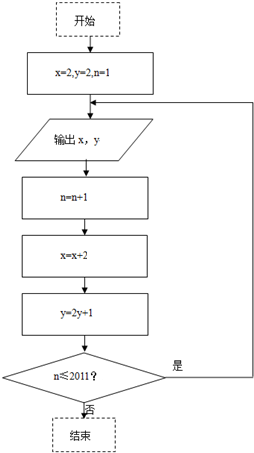 根据图所示的程序框图,将输出的x,y依次记为:x1,x2,…,x2011,y1,y2,…,y2011.
根据图所示的程序框图,将输出的x,y依次记为:x1,x2,…,x2011,y1,y2,…,y2011.