
【题目】已知函数f(x)是定义在R上的偶函数,且f(0)=0,当x>0时,
f(x)= ![]() .
.
(1)求函数f(x)的解析式;
(2)解不等式f(x2-1)>-2.
【答案】
(1)解:当x<0时,-x>0,则f(-x)=log ![]() (-x).
(-x).
因为函数f(x)是偶函数,所以f(-x)=f(x)=log ![]() (-x),
(-x),
所以函数f(x)的解析式为
(2)解:因为f(4)=log ![]() 4=-2,f(x)是偶函数,
4=-2,f(x)是偶函数,
所以不等式f(x2-1)>-2转化为f(|x2-1|)>f(4).
又因为函数f(x)在(0,+∞)上是减函数,
所以|x2-1|<4,解得- ![]() <x<
<x< ![]() ,
,
即不等式的解集为 ![]()
【解析】本题考查函数解析式的求法,以及根据性质求解不等式的问题。(1)根据函数的奇偶性找到在不同范围的解析式。(2)根据函数是偶函数把不等式进行转化,进而根据单调性脱去括号,得到不等式进行求解。


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,以
中,以 ![]() 为极点,
为极点, ![]() 轴非负半轴为极轴建立坐标系,已知曲线
轴非负半轴为极轴建立坐标系,已知曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() ,直线
,直线 ![]() 的参数方程为:
的参数方程为:  (
( ![]() 为参数),两曲线相交于
为参数),两曲线相交于 ![]() 两点.
两点.
(1)写出曲线 ![]() 的直角坐标方程和直线
的直角坐标方程和直线 ![]() 的普通方程;
的普通方程;
(2)若 ![]() 求
求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的最小正周期是
的最小正周期是 ![]() ,若将其图象向右平移
,若将其图象向右平移 ![]() 个单位后得到的图象关于
个单位后得到的图象关于 ![]() 轴对称,则函数
轴对称,则函数 ![]() 的图象( )
的图象( )
A.关于直线 ![]() 对称
对称
B.关于直线 ![]() 对称
对称
C.关于点 ![]() 对称
对称
D.关于点 ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( ) 
A.4
B.5
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,圆
中,圆 ![]() ,圆
,圆 ![]() .
.
(Ⅰ)在以 ![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,分别写出圆
轴正半轴为极轴的极坐标系中,分别写出圆 ![]() 的极坐标方程,并求出圆
的极坐标方程,并求出圆 ![]() 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);
(Ⅱ)求出 ![]() 与
与 ![]() 的公共弦的参数方程.
的公共弦的参数方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥 ![]() 的底面积
的底面积 ![]() 是边长为
是边长为 ![]() 的正三角形,
的正三角形, ![]() 点在侧面
点在侧面 ![]() 内的射影
内的射影 ![]() 为
为 ![]() 的垂心,二面角
的垂心,二面角 ![]() 的平面角的大小为
的平面角的大小为 ![]() ,则
,则 ![]() 的长为( )
的长为( )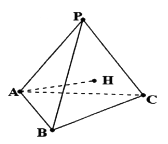
A.3
B.![]()
C.![]()
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线
轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为
![]() (
(![]() 为参数,
为参数, ![]() 为直线的倾斜角).
为直线的倾斜角).
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 有唯一的公共点,求角
有唯一的公共点,求角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中山某学校的场室统一使用“欧普照明”的一种灯管,已知这种灯管使用寿命![]() (单位:月)服从正态分布
(单位:月)服从正态分布![]() ,且使用寿命不少于
,且使用寿命不少于![]() 个月的概率为
个月的概率为![]() ,使用寿命不少于
,使用寿命不少于![]() 个月的概率为
个月的概率为![]() .
.
(1)求这种灯管的平均使用寿命![]() ;
;
(2)假设一间课室一次性换上![]() 支这种新灯管,使用
支这种新灯管,使用![]() 个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.
个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com