
【题目】已知三棱锥 ![]() 的底面积
的底面积 ![]() 是边长为
是边长为 ![]() 的正三角形,
的正三角形, ![]() 点在侧面
点在侧面 ![]() 内的射影
内的射影 ![]() 为
为 ![]() 的垂心,二面角
的垂心,二面角 ![]() 的平面角的大小为
的平面角的大小为 ![]() ,则
,则 ![]() 的长为( )
的长为( )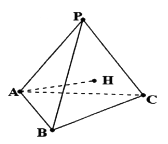
A.3
B.![]()
C.![]()
D.4
【答案】C
【解析】连结 ![]() 交
交 ![]() 于点
于点 ![]() ,连结
,连结 ![]() ,设
,设 ![]() 在底面
在底面 ![]() 内的射影为
内的射影为 ![]() ,则
,则 ![]() 平面
平面 ![]() ,连结
,连结 ![]() 交
交 ![]() 于点
于点 ![]()
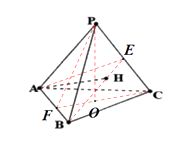
∵ ![]() 点在侧面
点在侧面 ![]() 内的射影
内的射影 ![]() 为
为 ![]() 的垂心
的垂心
∴ ![]() 平面
平面 ![]() ,
, ![]()
∴ ![]()
∵ ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]()
∴ ![]() 平面
平面 ![]()
∴ ![]()
∵ ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]()
∴ ![]()
∵ ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]()
∴ ![]() 平面
平面 ![]()
∵ ![]() 平面
平面 ![]()
∴ ![]()
同理可证 ![]()
∴ ![]() 是
是 ![]() 的垂心
的垂心
∴三棱锥 ![]() 为正三棱锥
为正三棱锥
∵三棱锥 ![]() 的底面
的底面 ![]() 是边长为
是边长为 ![]() 的正三角形
的正三角形
∴ ![]() ,
, ![]() ,则
,则 ![]()
∵二面角 ![]() 的平面角的大小为
的平面角的大小为 ![]()
∴ ![]() 为二面角
为二面角 ![]() 的平面角
的平面角
在 ![]() 中,
中, ![]() ,
, ![]()
∴ ![]()
在 ![]() 中,
中, ![]() ,
, ![]()
∴ ![]()
所以答案是:C
【考点精析】认真审题,首先需要了解棱锥的结构特征(侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方).


科目:高中数学 来源: 题型:
【题目】某厂为检验车间一生产线是否工作正常,现从生产线中随机抽取一批零件样本,测量尺寸(单位: ![]() )绘成频率分布直方图如图所示:
)绘成频率分布直方图如图所示: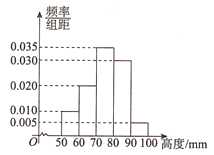
(Ⅰ)求该批零件样本尺寸的平均数 ![]() 和样本方差
和样本方差 ![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)若该批零件尺寸 ![]() 服从正态分布
服从正态分布 ![]() ,其中
,其中 ![]() 近似为样本平均数
近似为样本平均数 ![]() ,
, ![]() 近似为样本方差
近似为样本方差 ![]() ,利用该正态分布求
,利用该正态分布求 ![]() ;
;
(Ⅲ)若从生产线中任取一零件,测量尺寸为 ![]() ,根据
,根据 ![]() 原则判断该生产线是否正常?
原则判断该生产线是否正常?
附: ![]() ;若
;若 ![]() ,则
,则 ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且f(0)=0,当x>0时,
f(x)= ![]() .
.
(1)求函数f(x)的解析式;
(2)解不等式f(x2-1)>-2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 为坐标原点,
为坐标原点, ![]() ,
, ![]() 是椭圆
是椭圆 ![]() 上的点,且
上的点,且 ![]() ,设动点
,设动点 ![]() 满足
满足 ![]() .
.
(Ⅰ)求动点 ![]() 的轨迹
的轨迹 ![]() 的方程;
的方程;
(Ⅱ)若直线 ![]() 与曲线
与曲线 ![]() 交于
交于 ![]() 两点,求三角形
两点,求三角形 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() 的定义域为
的定义域为 ![]() ,若函数
,若函数 ![]() 满足下列两个条件,则称
满足下列两个条件,则称 ![]() 在定义域
在定义域 ![]() 上是闭函数.①
上是闭函数.① ![]() 在
在 ![]() 上是单调函数;②存在区间
上是单调函数;②存在区间 ![]() ,使
,使 ![]() 在
在 ![]() 上值域为
上值域为 ![]() .如果函数
.如果函数 ![]() 为闭函数,则
为闭函数,则 ![]() 的取值范围是.
的取值范围是.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左焦点
的左焦点![]() 和上顶点
和上顶点![]() 在直线
在直线![]() 上,
上, ![]() 为椭圆上位于
为椭圆上位于![]() 轴上方的一点且
轴上方的一点且![]() 轴,
轴, ![]() 为椭圆
为椭圆![]() 上不同于
上不同于![]() 的两点,且
的两点,且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】韩国民意调查机构“盖洛普韩国”2016年11月公布的民调结果显示,受“闺蜜门”时间影响,韩国总统朴槿惠的民意支持率持续下跌,在所调查的1000个对象中,年龄在[20,30)的群体有200人,支持率为0%,年龄在[30,40)和[40,50)的群体中,支持率均为3%;年龄在[50,60)和[60,70)的群体中,支持率分别为6%和13%,若在调查的对象中,除[20,30)的群体外,其余各年龄层的人数分布情况如频率分布直方图所示,其中最后三组的频数构成公差为100的等差数列.
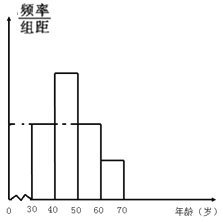
(1)依频率分布直方图求出图中各年龄层的人数
(2)请依上述支持率完成下表:
年龄分布 是否支持 | [30,40)和[40,50) | [50,60)和[60,70) | 合计 |
支持 | |||
不支持 | |||
合计 |
根据表中的数据,能否在犯错误的概率不超过0.001的前提下认为年龄与支持率有关?
附表:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() 参考数据:125×33=15×275,125×97=25×485)
参考数据:125×33=15×275,125×97=25×485)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com