练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数 的最小正周期是 ，若将其图象向右平移 个单位后得到的图象关于 轴对称，则函数 的图象（ ）
    A.关于直线 对称
    B.关于直线 对称
    C.关于点 对称
    D.关于点 对称

    【答案】D
    【解析】∵函数 的最小正周期是 ，∴ ，
    将其图象向右平移 个单位后得到的函数的表达式为 ，又 的图象关于 轴对称，
    ∴ ，∴ ,
    当 时， ，即
    易得： ， ,函数 的图象关于点 对称. 所以答案是：D
    【考点精析】利用函数y=Asin（ωx+φ）的图象变换对题目进行判断即可得到答案，需要熟知图象上所有点向左（右）平移个单位长度，得到函数的图象；再将函数的图象上所有点的横坐标伸长（缩短）到原来的倍（纵坐标不变），得到函数的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的倍（横坐标不变），得到函数的图象．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某市初三毕业生参加中考要进行体育测试，某实验中学初三（8）班的一次体育测试成绩的茎叶图和频率分布直方图都受到不同程度的涂黑，但可见部分如图，据此解答如下问题.

    （Ⅰ）求全班人数及中位数，并重新画出频率直方图；
    （Ⅱ）若要从分数在 之间的成绩中任取两个学生成绩分析学生得分情况，在抽取的学生中，求至少有一个分数在 之间的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂为检验车间一生产线是否工作正常，现从生产线中随机抽取一批零件样本，测量尺寸（单位： ）绘成频率分布直方图如图所示：

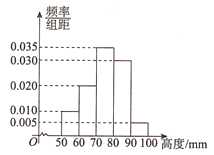
    （Ⅰ）求该批零件样本尺寸的平均数 和样本方差 （同一组中的数据用该组区间的中点值作代表）；
    （Ⅱ）若该批零件尺寸 服从正态分布 ，其中 近似为样本平均数 ， 近似为样本方差 ，利用该正态分布求 ；
    （Ⅲ）若从生产线中任取一零件，测量尺寸为 ，根据 原则判断该生产线是否正常？
    附： ；若 ，则 ， ， .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知y=f（x）是偶函数，而y=f（x+1）是奇函数，且对任意0≤x≤1，都有f（x）≥0，f（x）是增函数，则a=f（2010），b=f（ ），c=﹣f（ ）的大小关系是（ ）
    A.b＜c＜a
    B.c＜b＜a
    C.a＜c＜b
    D.a＜b＜c

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ， ．
    （1）当 时，求函数 的图象在 处的切线方程；
    （2）若函数 在定义域上为单调增函数．
    ①求 最大整数值；
    ②证明： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（某保险公司有一款保险产品的历史户获益率（获益率=获益÷保费收入）的频率分布直方图如图所示：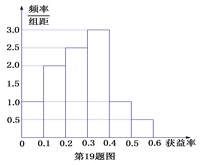

    （Ⅰ）试估计平均收益率；
    （Ⅱ）根据经验若每份保单的保费在 元的基础上每增加 元，对应的销量 （万份）与 （元）有较强线性相关关系，从历史销售记录中抽样得到如下 组 与 的对应数据：

    (元)

    销量 （万份）

    （ⅰ）根据数据计算出销量 （万份）与 （元）的回归方程为 ；
    （ⅱ）若把回归方程 当作 与 的线性关系，用（Ⅰ）中求出的平均获益率估计此产品的获益率，每份保单的保费定为多少元时此产品可获得最大获益，并求出该最大获益.
    参考公示：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】执行如图的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为（ ）

    A.5
    B.4
    C.3
    D.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)是定义在R上的偶函数，且f(0)＝0，当x>0时，
    f(x)＝ .
    （1）求函数f(x)的解析式；
    （2）解不等式f(x2－1)>－2.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为（为参数），在以原点为极点， 轴正半轴为极轴的极坐标系中，直线的极坐标方程为．

    （1）求曲线的普通方程和直线的倾斜角；

    （2）设点，直线和曲线交于两点，求的值．

    查看答案和解析>>

    同步练习册答案