
设二次函数 ,对任意实数
,对任意实数 ,有
,有 恒成立;数列
恒成立;数列 满足
满足 .
.
(1)求函数 的解析式和值域;
的解析式和值域;
(2)试写出一个区间 ,使得当
,使得当 时,数列
时,数列 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;
(3)已知 ,是否存在非零整数
,是否存在非零整数 ,使得对任意
,使得对任意 ,都有
,都有
 恒成立,若存在,
恒成立,若存在,
求之;若不存在,说明理由.
解:(1)由 恒成立等价于
恒成立等价于 恒成立,…1分
恒成立,…1分
从而得: ,化简得
,化简得 ,从而得
,从而得 ,
,
所以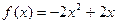 ,………3分
,………3分
其值域为 .…………………4分
.…………………4分
(2)解:当 时,数列
时,数列 在这个区间上是递增数列,证明如下:
在这个区间上是递增数列,证明如下:
设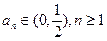 ,则
,则 ,
,
所以对一切 ,均有
,均有 ;………………7分
;………………7分

从而得 ,即
,即 ,所以数列
,所以数列 在区间
在区间 上是递增数列…10分
上是递增数列…10分
注:本题的区间也可以是 、
、 、
、 等无穷多个.
等无穷多个.
另解:若数列 在某个区间上是递增数列,则
在某个区间上是递增数列,则
即
 …7分
…7分
又当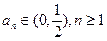 时,
时, ,
,
∴对一切 ,均有
,均有 且
且 ,
,
∴数列 在区间
在区间 上是递增数列.…………………………10分
上是递增数列.…………………………10分
(3)(文科)由(2)知 ,从而
,从而 ;
; ,
,
即 ; ………12分
; ………12分
令 ,则有
,则有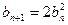 且
且 ;
;
从而有 ,可得
,可得 ,
,
∴数列 是以
是以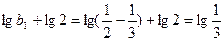 为首项,公比为
为首项,公比为 的等比数列,………14分
的等比数列,………14分
从而得 ,即
,即 ,
,
∴  ,
,
∴ ,∴
,∴ , …16分
, …16分
∴,
 . ………………………18分
. ………………………18分
(3)(理科)由(2)知 ,从而
,从而 ;
; ,
,
即 ;………12分
;………12分
令 ,则有
,则有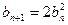 且
且 ;
;
从而有 ,可得
,可得 ,所以数列
,所以数列 是
是 为首项,公比为
为首项,公比为 的等比数列,…………………14分
的等比数列,…………………14分
从而得 ,即
,即 ,
,
所以  ,
,
所以 ,所以
,所以 解析
解析


科目:高中数学 来源: 题型:解答题
(12分)已知二次函数f (x)= ,设方程f (x)
,设方程f (x)
=x的两个实根为x1和x2.
(1)如果x1<2<x2<4,且函数f (x)的对称轴为x=x0,求证:x0>—1;
(2)如果∣x1∣<2,,∣x2—x1∣=2,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业生产一种产品时,固定成本为5000元,而每生产100台产品时直接消耗成本要增加2500元,市场对此商品年需求量为500台,销售的收入函数为R(x)=5x-x2(万元)(0≤x≤5),其中x是产品售出的数量(单位:百台)
(1)把利润表示为年产量的函数;
(2)年产量多少时,企业所得的利润最大?
(3)年产量多少时,企业才不亏本?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
定义域为R,且对任意实数 都满足不等式
都满足不等式 的所有函数
的所有函数 组成的集合记为M,例如,函数
组成的集合记为M,例如,函数 。
。
(1)已知函数 ,证明:
,证明:
 ;
;
(2)写出一个函数 ,使得
,使得 ,并说明理由;
,并说明理由;
(3)写出一个函数
 ,使得数列极限
,使得数列极限
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,当
,当 恒成立的a的最小值为k,存在n个
恒成立的a的最小值为k,存在n个
正数 ,且
,且 ,任取n个自变量的值
,任取n个自变量的值
(I)求k的值;
(II)如果
(III)如果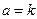 ,且存在n个自变量的值
,且存在n个自变量的值 ,使
,使 ,求证:
,求证:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com