
已知函数 的定义域为
的定义域为 。
。
(1)求函数 的值域;
的值域;
(2)求函数 的反函数。(12分)
的反函数。(12分)
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
在平面直角坐标系 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为
的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为 .
.
(I)求实数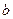 的取值范围;
的取值范围;
(II)求圆 的一般方程;
的一般方程;
(III)圆 是否经过某个定点(其坐标与
是否经过某个定点(其坐标与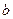 无关)?若存在,请求出点点的坐标;若不存在,请说明理由.
无关)?若存在,请求出点点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)
某民营企业生产A、B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图一所示;B产品的利润与投资的算术平方根成正比,其关系如图二所示(利润与投资单位:万元).
(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)已知集合A={a1,a2,a3,a4},B={0,1,2,3},f是从A到B的映射.
(1)若B中每一元素都有原象,这样不同的f有多少个?
(2)若B中的元素0必无原象,这样的f有多少个?
(3)若f满足f(a1)+f(a2)+f(a3)+f(a4)=4,这样的f又有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知函数 , 其中
, 其中 为常数,且函数
为常数,且函数 图像过原点.
图像过原点.
(1) 求 的值;
的值;
(2) 证明函数 在[0,2]上是单调递增函数;
在[0,2]上是单调递增函数;
(3) 已知函数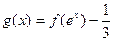 , 求函数
, 求函数 的零点
的零点
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数: ,其中
,其中 是仪器的月产量.
是仪器的月产量.
(1)将利润 元表示为月产量
元表示为月产量 台的函数;
台的函数;
(2)当月产量为何值时,公司所获得利润最大?最大利润是多少?(总收益=总成本+利润)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设二次函数 ,对任意实数
,对任意实数 ,有
,有 恒成立;数列
恒成立;数列 满足
满足 .
.
(1)求函数 的解析式和值域;
的解析式和值域;
(2)试写出一个区间 ,使得当
,使得当 时,数列
时,数列 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;
(3)已知 ,是否存在非零整数
,是否存在非零整数 ,使得对任意
,使得对任意 ,都有
,都有
 恒成立,若存在,
恒成立,若存在,
求之;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com