
【题目】在四棱锥![]() 中,底面
中,底面![]() 是正方形,
是正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 、
、![]() 的中点,对于平面
的中点,对于平面![]() 截四棱锥
截四棱锥![]() 所得的截面多边形,有以下三个结论:
所得的截面多边形,有以下三个结论:
①截面的面积等于![]() ;
;
②截面是一个五边形;
③截面只与四棱锥![]() 四条侧棱中的三条相交.
四条侧棱中的三条相交.
其中,所有正确结论的序号是______.
【答案】②③
【解析】
取![]() 的中点
的中点![]() ,
,![]() 的四等分点
的四等分点![]() ,顺次连接
,顺次连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,则平面
,则平面![]() 即为过
即为过![]() 、
、![]() 、
、![]() 的平面截四棱锥
的平面截四棱锥![]() 所得截面,计算出截面面积,根据截面形状可判断命题①②③的正误.
所得截面,计算出截面面积,根据截面形状可判断命题①②③的正误.
取![]() 的中点
的中点![]() ,
,![]() 的四等分点
的四等分点![]() ,顺次连接
,顺次连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
则平面![]() 即为过
即为过![]() 、
、![]() 、
、![]() 的平面截四棱锥
的平面截四棱锥![]() 所得截面,如下图所示:
所得截面,如下图所示:
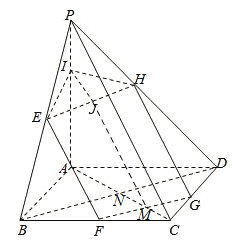
在四棱锥![]() 中,底面
中,底面![]() 是正方形,
是正方形,![]() 底面
底面![]() ,
,![]() ,
,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() 且
且![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,
![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() ,
,
同理可得![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为正方形,则
为正方形,则![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
则![]() ,所以,四边形
,所以,四边形![]() 为矩形,其面积为
为矩形,其面积为![]() ,
,
设![]() ,
,![]() ,则
,则![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,
![]() 的边
的边![]() 上的高为
上的高为![]() ,
,
![]() 的面积为
的面积为![]() .
.
所以,截面面积为![]() ,命题①错误;
,命题①错误;
该截面是一个五边形,命题②正确;
由图可知,截面与四棱锥![]() 侧棱
侧棱![]() 、
、![]() 、
、![]() 相交,命题③正确.
相交,命题③正确.
故答案为:②③.


科目:高中数学 来源: 题型:
【题目】近些年随着我国国民消费水平的升级,汽车产品已经逐渐进入千家万户,但是我国的城市发展水平并不能与汽车保有量增速形成平衡,城市交通问题越发突出,因此各大城市相继出现了购车限号上牌的政策.某城市采用摇号买车的限号上牌方式,申请人提供申请,经审查合格后,确认申请编码为有效编码,这时候就可以凭借申请编码参加每月一次的摇号.假设该城市有20万人参加摇号,每个月有2万个名额,每个月摇上的人退出摇号,没有摇上的人继续下个月摇号.
(1)平均每个人摇上号需要多长时间?
(2)如果每个月都有2万人补充进摇号队伍,以每个人进入摇号的月份算第一个月,他摇到号的月份设为随机变量![]() .
.
①证明:![]() 为等比数列;
为等比数列;
②假设该项政策连续实施36个月,小王是第一个月就参加摇号的人,记小王参.加摇号的次数为![]() ,试求
,试求![]() 的数学期望(精确到0.01).
的数学期望(精确到0.01).
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:只要
满足:只要![]() ,必有
,必有![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)若![]() 具有性质
具有性质![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是等比数列,
是等比数列,![]() ,
,![]() ,
,![]() .判断
.判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(3)设![]() 是无穷数列,已知
是无穷数列,已知![]() .求证:“对任意
.求证:“对任意![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某款电视机的寿命,研究人员对该款电视机进行了相应的测试,将得到的数据分组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并统计如图所示:
,并统计如图所示:
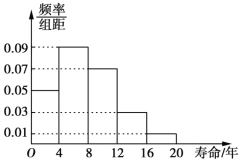
并对不同性别的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
愿意购买该款电视机 | 不愿意购买该款电视机 | 总计 | |
男性 | 800 | 1000 | |
女性 | 600 | ||
总计 | 1200 |
(1)根据图中的数据,试估计该款电视机的平均寿命;
(2)根据表中数据,能否在犯错误的概率不超过0.001的前提下认为“是否愿意购买该款电视机”与“市民的性别”有关;
(3)以频率估计概率,若在该款电视机的生产线上随机抽取4台,记其中寿命不低于4年的电视机的台数为X,求X的分布列及数学期望.
参考公式及数据: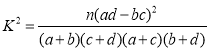 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,平面四边形![]() 中,
中,![]() 为
为![]() 上一点,
上一点,![]() 和
和![]() 均为等边三角形,
均为等边三角形,![]()
![]() 分别是
分别是![]() 和
和![]() 的中点,将四边形
的中点,将四边形![]() 沿
沿![]() 向上翻折至四边形
向上翻折至四边形![]() 的位置,使二面角
的位置,使二面角![]() 为直二面角,如图2所示.
为直二面角,如图2所示.
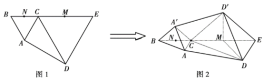
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校6个学生的数学和物理成绩如下表:
学生的编号 | 1 | 2 | 3 | 4 | 5 | 6 |
数学 | 89 | 87 | 79 | 81 | 78 | 90 |
物理 | 79 | 75 | 77 | 73 | 72 | 74 |
(1)若在本次考试中,规定数学在80分以上(包括80分)且物理在75分以上(包括75分)的学生为理科小能手.从这6个学生中抽出2个学生,设![]() 表示理科小能手的人数,求
表示理科小能手的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系,在上述表格是正确的前提下,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示物理成绩,求
表示物理成绩,求![]() 与
与![]() 的回归方程.
的回归方程.
参考数据和公式:![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com