
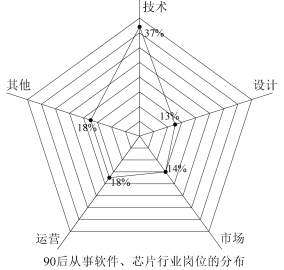
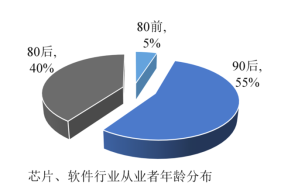
【题目】中兴、华为事件暴露了我国计算机行业中芯片、软件两大短板,为防止“卡脖子”事件的再发生,科技专业人才就成了决胜的关键.为了解我国在芯片、软件方面的潜力,某调查机构对我国若干大型科技公司进行调查统计,得到了这两个行业从业者的年龄分布的饼形图和“90后”从事这两个行业的岗位分布雷达图,则下列说法中不一定正确的是( )
A.芯片、软件行业从业者中,“90后”占总人数的比例超过50%
B.芯片、软件行业中从事技术设计岗位的“90后”人数超过总人数的25%
C.芯片、软件行业从事技术岗位的人中,“90后”比“80后”多
D.芯片、软件行业中,“90后”从事市场岗位的人数比“80前“的总人数多
【答案】C
【解析】
根据图表信息,整合数据,逐项判断即可得解.
对于选项A,芯片、软件行业从业者中“90后”占总人数的55%,故选项A正确;
对于选项B,芯片、软件行业中从事技术、设计岗位的“90后”占总人数的(37%+13%)×55%=27.5%,故选项B正确;
对于选项C,芯片、软件行业中从事技术岗位的“90后”占总人数的37%×55%=20.35%,“80后”占总人数的40%,但从事技术的“80后”占总人数的百分比不知道,无法确定二者人数多少,故选项C错误;
对于选项D,芯片、软件行业中从事市场岗位的“90后”占总人数的14%×55%=7.7%、“80前”占总人数的5%,故选项D正确.
故选:C.


科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC–A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点.过B1C1和P的平面交AB于E,交AC于F.
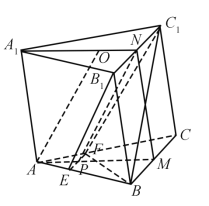
(1)证明:AA1//MN,且平面A1AMN⊥平面EB1C1F;
(2)设O为△A1B1C1的中心,若AO=AB=6,AO//平面EB1C1F,且∠MPN=![]() ,求四棱锥B–EB1C1F的体积.
,求四棱锥B–EB1C1F的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义城为R的函数![]() ,若满足:①
,若满足:①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() 且
且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.下列函数是“偏对称函数”的是( )
为“偏对称函数”.下列函数是“偏对称函数”的是( )
A.![]() B.
B.![]()
C.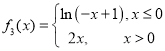 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载每个人每日健步的步数,从而为科学健身提供一定的帮助.某市工会为了解该市市民每日健步走的情况,从本市市民中随机抽取了2000名市民(其中不超过40岁的市民恰好有1000名),利用手机计步软件统计了他们某天健步的步数,并将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 九组(单位;千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如图,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
九组(单位;千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如图,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
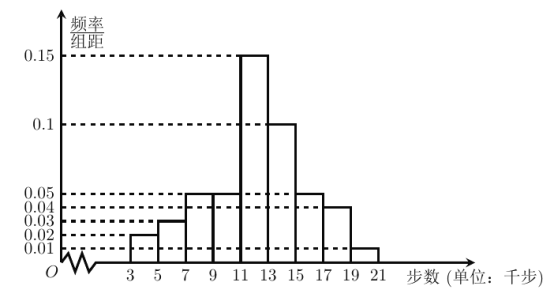
分组(单位 千步) |
|
|
|
|
|
|
|
|
|
频数 | 10 | 20 | 20 | 30 | 400 | 200 | 200 | 100 | 20 |
(1)现规定,日健步步数不低于13000步的为“健步达人”,填写下面列联表,并根据列联表判断能否有99.9%的把握认为是否为“健步达人”与年龄有关;
健步达人 | 非健步达人 | 总计 | |
40岁以上的市民 | |||
不超过40岁的市民 | |||
总计 |
(2)利用样本平均数和中位数估计该市不超过40岁的市民日健步步数(单位:千步)的平均数和中位数;
(3)若日健步步数落在区间![]() 内,则可认为该市民”运动适量”,其中
内,则可认为该市民”运动适量”,其中![]() ,
,![]() 分别为样本平均数和样本标准差,计算可求得频率分布直方图中数据的标准差
分别为样本平均数和样本标准差,计算可求得频率分布直方图中数据的标准差![]() 约为3.64.若一市民某天的健步步数为2万步,试判断该市民这天是否“运动适量”?
约为3.64.若一市民某天的健步步数为2万步,试判断该市民这天是否“运动适量”?
参考公式: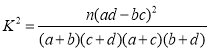
![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,且asinB![]() bcosA+a=bcosC+ccosB.
bcosA+a=bcosC+ccosB.
(1)求A;
(2)若a![]() ,点D在BC上,且AD⊥AC,当△ABC的周长取得最大值时,求BD的长.
,点D在BC上,且AD⊥AC,当△ABC的周长取得最大值时,求BD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区![]() 的
的![]() 天日落和夜晚天气,得到如下
天日落和夜晚天气,得到如下![]() 列联表:
列联表:
夜晚天气日落云里走 | 下雨 | 未下雨 |
出现 |
|
|
未出现 |
|
|
参考公式: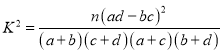 .
.
临界值表:
|
|
|
|
|
|
|
|
|
|
(1)根据上面的列联表判断能否有![]() 的把握认为“当晚下雨”与“‘日落云里走’出现”有关?
的把握认为“当晚下雨”与“‘日落云里走’出现”有关?
(2)小波同学为进一步认识其规律,对相关数据进行分析,现从上述调查的“夜晚未下雨”天气中按分层抽样法抽取![]() 天,再从这
天,再从这![]() 天中随机抽出
天中随机抽出![]() 天进行数据分析,求抽到的这
天进行数据分析,求抽到的这![]() 天中仅有
天中仅有![]() 天出现“日落云里走”的概率.
天出现“日落云里走”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
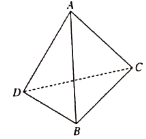
【题目】现有一副斜边长为10的直角三角板,将它们斜边![]() 重合,若将其中一个三角板沿斜边折起形成三棱锥
重合,若将其中一个三角板沿斜边折起形成三棱锥![]() ,如图所示,已知
,如图所示,已知![]() ,
,![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积为______;该三棱锥体积的最大值为_______.
的外接球的表面积为______;该三棱锥体积的最大值为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象如图所示,给出四个函数:①
的图象如图所示,给出四个函数:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,又给出四个函数的图象,则正确的匹配方案是( ).
,又给出四个函数的图象,则正确的匹配方案是( ).
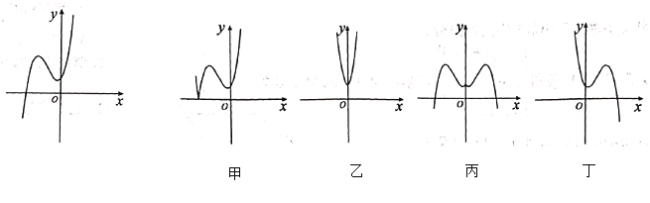
A.①-甲,②-乙,③-丙,④-丁B.②-甲,①-乙,③-丙,④-丙
C.①-甲,③-乙,④-丙,②-丁D.①-甲,④-乙,③-丙,②-丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com