
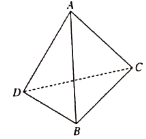
【题目】现有一副斜边长为10的直角三角板,将它们斜边![]() 重合,若将其中一个三角板沿斜边折起形成三棱锥
重合,若将其中一个三角板沿斜边折起形成三棱锥![]() ,如图所示,已知
,如图所示,已知![]() ,
,![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积为______;该三棱锥体积的最大值为_______.
的外接球的表面积为______;该三棱锥体积的最大值为_______.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】中兴、华为事件暴露了我国计算机行业中芯片、软件两大短板,为防止“卡脖子”事件的再发生,科技专业人才就成了决胜的关键.为了解我国在芯片、软件方面的潜力,某调查机构对我国若干大型科技公司进行调查统计,得到了这两个行业从业者的年龄分布的饼形图和“90后”从事这两个行业的岗位分布雷达图,则下列说法中不一定正确的是( )
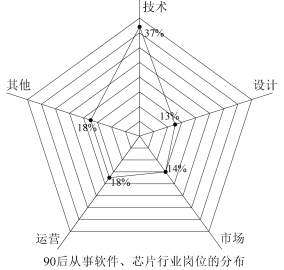
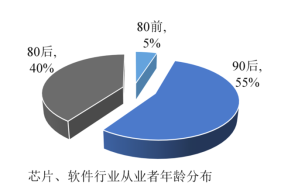
A.芯片、软件行业从业者中,“90后”占总人数的比例超过50%
B.芯片、软件行业中从事技术设计岗位的“90后”人数超过总人数的25%
C.芯片、软件行业从事技术岗位的人中,“90后”比“80后”多
D.芯片、软件行业中,“90后”从事市场岗位的人数比“80前“的总人数多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某国营企业集团公司现有员工1000名,平均每人每年创造利润10万元.为了激化内部活力,增强企业竞争力,集团公司董事会决定优化产业结构,调整出![]() (
(![]() )名员工从事第三产业;调整后,他们平均每人每年创造利润
)名员工从事第三产业;调整后,他们平均每人每年创造利润![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() %.
%.
(Ⅰ)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(Ⅱ)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则实数![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为2,点
的棱长为2,点![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() 的中点,下列结论中,其中正确的个数是( )
的中点,下列结论中,其中正确的个数是( )
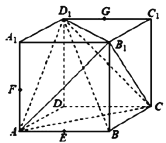
①过![]() ,
,![]() ,
,![]() 三点作正方体的截面,所得截面为正六边形;
三点作正方体的截面,所得截面为正六边形;
②![]() 平面
平面![]() ;
;
③![]() 平面
平面![]() ;
;
④异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ;
;
⑤四面体![]() 的体积等于
的体积等于![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )



A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果某企业每月生猪的死亡率不超过百分之一,则该企业考核为优秀.现获得某企业2019年1月到8月的相关数据如下表所示:
月份 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 |
月养殖量/千只 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 12 |
月利润/十万元 | 3.6 | 4.1 | 4.4 | 5.2 | 6.2 | 7.5 | 7.9 | 9.1 |
生猪死亡数最/只 | 29 | 37 | 49 | 53 | 77 | 98 | 126 | 145 |
(1)求出月利润;y(十万元)关于月养殖量x(千只)的线性回归方程(精确到0.01);
(2)若2019年9月份该企业月养殖量为1.4万只,请你预估该月月利润是多少万元;
(3)从该企业2019年1月到8月这8个月中任意选取3个月,用X表示3个月中该企业考核获得优秀的个数,求X的分布列和数学期望./p>
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
附:线性回归方程![]() 中,
中,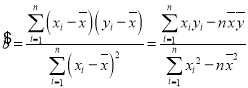 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人玩掷正方体骰子走跳棋的游戏,已知骰子每面朝上的概率都是![]() ,棋盘上标有第0站,第1站,第2站,……,第100站.一枚棋子开始在第0站,选手每掷一次骰子,棋子向前跳动一次,若掷出朝上的点数为1或2,棋子向前跳两站;若掷出其余点数,则棋子向前跳一站,直到跳到第99站或第100站时,游戏结束;设游戏过程中棋子出现在第
,棋盘上标有第0站,第1站,第2站,……,第100站.一枚棋子开始在第0站,选手每掷一次骰子,棋子向前跳动一次,若掷出朝上的点数为1或2,棋子向前跳两站;若掷出其余点数,则棋子向前跳一站,直到跳到第99站或第100站时,游戏结束;设游戏过程中棋子出现在第![]() 站的概率为
站的概率为![]() .
.
(1)当游戏开始时,若抛掷均匀骰子3次后,求棋子所走站数之和X的分布列与数学期望;
(2)证明:![]() ;
;
(3)若最终棋子落在第99站,则记选手落败,若最终棋子落在第100站,则记选手获胜,请分析这个游戏是否公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com