
分析 由于(1+ax)5(1-2x)4=$(1+{∁}_{5}^{1}ax+{∁}_{5}^{2}{a}^{2}{x}^{2}+…)$$(1-{∁}_{4}^{1}×2x+{∁}_{4}^{2}×4{x}^{2}+…)$,即可得出.
解答 解:(1+ax)5(1-2x)4=$(1+{∁}_{5}^{1}ax+{∁}_{5}^{2}{a}^{2}{x}^{2}+…)$$(1-{∁}_{4}^{1}×2x+{∁}_{4}^{2}×4{x}^{2}+…)$,
由于展开式中x2的系数为-16,则${∁}_{4}^{2}$×4+$-2{∁}_{4}^{1}$×${∁}_{5}^{1}a$+${∁}_{5}^{2}{a}^{2}$=-16,
化为:a2-4a+4=0,
解得a=2.
故答案为:2.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(文)试卷(解析版) 题型:选择题
已知函数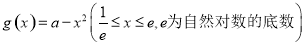 与
与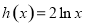 的图象上存在关于
的图象上存在关于 轴对称的点,则实数
轴对称的点,则实数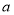 的取值范围是( )
的取值范围是( )
A.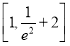 B.
B.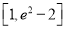 C.
C.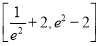 D.
D.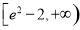
查看答案和解析>>
科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(文)试卷(解析版) 题型:解答题
某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.

(1)求分数在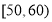 的频率及全班人数;
的频率及全班人数;
(2)求分数在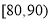 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中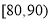 间矩形的高;
间矩形的高;
(3)若要从分数在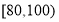 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在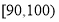 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-∞,-1) | C. | (3,+∞) | D. | (log38,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知椭圆Ⅰ与椭圆Ⅱ有公共左顶点A与公共左焦点F,且椭圆Ⅰ的长轴长是椭圆Ⅱ的长釉长的k(k>1,且k为常数)倍,则椭圆Ⅰ的离心率的取值范围是$(1-\frac{1}{k},1)$.
如图,已知椭圆Ⅰ与椭圆Ⅱ有公共左顶点A与公共左焦点F,且椭圆Ⅰ的长轴长是椭圆Ⅱ的长釉长的k(k>1,且k为常数)倍,则椭圆Ⅰ的离心率的取值范围是$(1-\frac{1}{k},1)$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com