
 如图,已知椭圆Ⅰ与椭圆Ⅱ有公共左顶点A与公共左焦点F,且椭圆Ⅰ的长轴长是椭圆Ⅱ的长釉长的k(k>1,且k为常数)倍,则椭圆Ⅰ的离心率的取值范围是$(1-\frac{1}{k},1)$.
如图,已知椭圆Ⅰ与椭圆Ⅱ有公共左顶点A与公共左焦点F,且椭圆Ⅰ的长轴长是椭圆Ⅱ的长釉长的k(k>1,且k为常数)倍,则椭圆Ⅰ的离心率的取值范围是$(1-\frac{1}{k},1)$. 分析 设椭圆II的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率为e=$\frac{c}{a}$.椭圆I的标准方程为:$\frac{(x-{x}_{0})^{2}}{{a}_{1}^{2}}$+$\frac{{y}^{2}}{{b}_{1}^{2}}$=1,设离心率为e1.由于ka-x0=a,可得x0=(k-1)a.于是e1=$\frac{(k-1)a+c}{ka}$=1+$\frac{1}{k}$(e-1),根据0<e<1即可得出.
解答 解:设椭圆II的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率为e=$\frac{c}{a}$.
椭圆I的标准方程为:$\frac{(x-{x}_{0})^{2}}{{a}_{1}^{2}}$+$\frac{{y}^{2}}{{b}_{1}^{2}}$=1,设离心率为e1.
则ka-x0=a,∴x0=(k-1)a.
∴e1=$\frac{(k-1)a+c}{ka}$=1+$\frac{1}{k}$(e-1),
∵0<e<1,
∴e1∈$(1-\frac{1}{k},1)$.
故答案为:$(1-\frac{1}{k},1)$.
点评 本题考查了椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:选择题
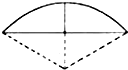 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为$\frac{2π}{3}$,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )
《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为$\frac{2π}{3}$,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )| A. | 6平方米 | B. | 9平方米 | C. | 12平方米 | D. | 15平方米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com