
分析 (1)由题意可得$\overrightarrow{a}$=(-2,-1),$\overrightarrow{b}$=(1,-λ),运用向量共线的坐标表示,解方程即可得到;
(2)运用向量垂直的条件:数量积为0,计算即可得到所求值.
解答 解:(1)由$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是两个互相垂直的单位向量,
可设$\overrightarrow{a}$=(-2,-1),$\overrightarrow{b}$=(1,-λ),
若$\overrightarrow{a}$∥$\overrightarrow{b}$,即有-1=2λ,解得λ=-$\frac{1}{2}$;
(2)若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则-2×1+(-1)×(-λ)=0,
解得λ=2.
故答案为:-$\frac{1}{2}$,反向,-2.
点评 本题考查向量的共线和垂直的条件:数量积为0,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | a、b、c成等比数列 | B. | a、b、c成等差数列 | ||
| C. | a2、b2、c2成等比数列 | D. | a2、b2、c2成等差数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
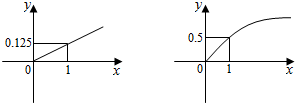 某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com