
分析 (1)利用导数求出x=2处的斜率,根据点斜式写出切线方程;
(2)要使对?x∈[-1,$\frac{1}{2}$],不等式f(x)<a2恒成立,即f(x)max<a2;利用导数判断单调性求出f(x)的最大值即可.
解答 解:(1)由a=1,所以f(x)=x3-$\frac{3}{2}{x}^{2}$+1,f(2)=3;
又f'(x)=3x2-3x,所以k=f'(x)=6;
所以切线方程为y-3=6(x-2);
切线方程为:y=6x-9.
(2)f'(x)=3ax2-3x
令f'(x)=3ax2-3x=0;⇒x1=0,x2=$\frac{1}{a}$;
因为a>0,所以y=f(x)在(-∞,0],[$\frac{1}{a}$,+∞)递增,在(0,$\frac{1}{a}$)递减;
要使对?x∈[-1,$\frac{1}{2}$],不等式f(x)<a2恒成立,即f(x)max<a2,
1°.当$\frac{1}{2}≤\frac{1}{a}$时,即0<a≤2时,y=f(x)在[-1,0]递增,在(0,$\frac{1}{2}$)递减;
f(x)max=f(0)=1<a2 所以1<a≤2;
2°.当$\frac{1}{a}<\frac{1}{2}$时,即a>2时,y=f(x)在[-1,0]递增,在(0,$\frac{1}{a}$)递减,在[$\frac{1}{a}$,$\frac{1}{2}$]递增;
$f(x)_{max}=max\{f(0),f(\frac{1}{2})\}$,f($\frac{1}{2}$)=$\frac{a+5}{8}$=f(0)=1⇒a=3;
①当2<a<3时,$f(x)_{max}=max\{f(0),f(\frac{1}{2})\}$=f(0)=1<a2 所以2<a<3;
②当a≥3时,$f(x)_{max}=max\{f(0),f(\frac{1}{2})\}$=f($\frac{1}{2}$)<a2,
即8a2-a-5>0 对?a≥3都成立;
综合1,2得:a>1
点评 本题主要考查了利用导数求斜率,直线方程以及利用导数判断函数的单调性与最值等知识点,属中等题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,4] | B. | (-∞,4] | C. | [3,+∞) | D. | (-∞,1]∪[4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinα)>f(cosβ) | B. | f(sinα)>f(sinβ) | C. | f(sinα)<f(cosβ) | D. | f(cosα)>f(cosβ) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
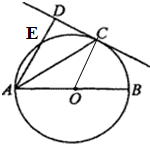 如图,已知AB是圆O的直径,直线CD与圆O相切于点C,AC平分∠DAB,AD与圆O相交于点E
如图,已知AB是圆O的直径,直线CD与圆O相切于点C,AC平分∠DAB,AD与圆O相交于点E查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>0 | B. | a≥0 | C. | $0<a≤\frac{2}{e}$ | D. | $0≤a≤\frac{2}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com