
设 为实数,函数
为实数,函数 .
.
(1)求 的单调区间与极值;
的单调区间与极值;
(2)求证:当 且
且 时,
时, .
.
(1)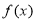 在
在 上减,在
上减,在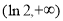 上增;当
上增;当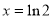 时,
时, 取极小值
取极小值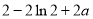 (2)见解析
(2)见解析
【解析】
试题分析:本题考查函数的单调区间及极值的求法和不等式的证明,具体涉及到导数的性质、函数增减区间的判断、极值的计算和不等式性质的应用.
(1)由 ,知
,知 ,令
,令 ,得到
,得到
 ,列表讨论能求出f(x)的单调区间区间及极值.
,列表讨论能求出f(x)的单调区间区间及极值.
(2)设 ,于是
,于是 ,由(1)知当a>ln2-1时,
,由(1)知当a>ln2-1时,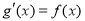 最小值为
最小值为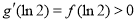 .于是对任意x∈R,都有
.于是对任意x∈R,都有 ,所以g(x)在
,所以g(x)在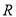 单调递增.由此能够证明
单调递增.由此能够证明 .
.
试题解析:(1)由 ,知
,知 ,令
,令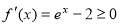 ,得到
,得到
 ,故
,故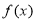 在
在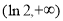 上单调递增,在
上单调递增,在 上单调递减,当
上单调递减,当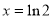 时,
时,

 ,即
,即 取极小值
取极小值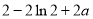
(2)设函数 ,则
,则 ,由(1)知
,由(1)知 的极小值也是最小值为
的极小值也是最小值为 ,当
,当 时,
时, ,即在
,即在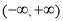 内,
内, 的最小值
的最小值 ,
, 恒成立,即在
恒成立,即在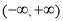 内
内 ,
,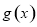 在
在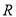 单调递增,
单调递增, 即
即 即
即
考点:函数的单调区间及极值的求法和不等式的证明


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源:2015届山西省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
点P是曲线x2-y-2ln =0上任意一点,则点P到直线4x+4y+1=0的最短距离是( )
=0上任意一点,则点P到直线4x+4y+1=0的最短距离是( )
A. (1-ln 2) B.
(1-ln 2) B. (1+ln 2) C.
(1+ln 2) C.
 D.
D. (1+ln 2)
(1+ln 2)
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二3月月考文科数学试卷(解析版) 题型:选择题
下表是某厂1~4月份用水量(单位:百吨)的一组数据:

由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是=-0.7x+a,则a等于( )
A.10.5 B.5.15 C.5.2 D.5.25
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二暑假作业四数学试卷(解析版) 题型:选择题
已知抛物线 的准线与双曲线
的准线与双曲线 交于A,B两点,点F为抛物线的焦点,若
交于A,B两点,点F为抛物线的焦点,若 为直角三角形,则双曲线的离心率是
为直角三角形,则双曲线的离心率是
A. B.
B. C.2 D.3
C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com