
分析 作差,判断2$f(\frac{{x}_{1}{+x}_{2}}{2})$-f(x1)-f(x2)的符号即可.
解答 解:2$f(\frac{{x}_{1}{+x}_{2}}{2})$-f(x1)-f(x2)
=2•${(\frac{{x}_{1}{+x}_{2}}{2})}^{2}$+x1+x2-${{x}_{1}}^{2}$-x1-${{x}_{2}}^{2}$-x2
=-$\frac{1}{2}$${{x}_{1}}^{2}$+x1x2-$\frac{1}{2}$${{x}_{2}}^{2}$
=-$\frac{1}{2}$${{(x}_{1}{-x}_{2})}^{2}$≤0,
∴f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$;
故答案为:①.
点评 本题考查了函数值的大小比较,考查二次函数的性质,是一道基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{12}{5}$ | B. | $\frac{12}{5}$ | C. | ±$\frac{12}{5}$ | D. | ±$\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
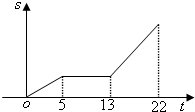 某同学来学校上学,时间t(分钟)与路程s(米)的函数关系如图所示,现有如下几种说法:
某同学来学校上学,时间t(分钟)与路程s(米)的函数关系如图所示,现有如下几种说法:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com