
分析 先求出基本事件总数,再求出选取的学生会干部人数不少于2人包含的基本事件个数,由此能求出选取的学生会干部人数不少于2人的概率.
解答 解:某志愿团由10名同学构成,其中3名学生会干部,现从中随机选取4名同学去支教,
基本事件总数n=C${\;}_{10}^{4}$=210,
选取的学生会干部人数不少于2人包含的基本事件个数m=${C}_{7}^{2}{C}_{3}^{2}$+${C}_{7}^{1}{C}_{3}^{3}$=70,
∴选取的学生会干部人数不少于2人的概率p=$\frac{m}{n}$=$\frac{70}{210}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 0.384 | B. | 0.096 | C. | 0.616 | D. | 0.904 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
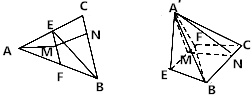 如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF-CB,M为EF中点.
如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF-CB,M为EF中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若下一销售季再投入5百万元广告费,则估计销售额约可达47.1百万元 | |
| B. | 已知统计数据中的平均销售额为41.4百万元,则平均广告费为4百万元 | |
| C. | 广告费用x和销售额y之间的相关系数不能确定正负,但其绝对值趋于1 | |
| D. | 5.7的含义是广告费用每增加1百万元,销售额大约增长5.7百万元左右 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (-∞,0] | C. | [1,+∞) | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
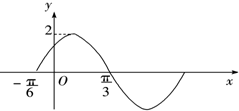 函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.
函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com