
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 2011-2015年北京市职工年平均工资(税前:单位:元) | |
| 时间 | 平均年薪 |
| 2011 | 56061 |
| 2012 | 62677 |
| 2013 | 69521 |
| 2014 | 77560 |
| 2015 | 85038 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
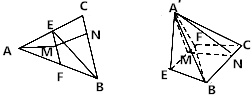 如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF-CB,M为EF中点.
如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF-CB,M为EF中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若下一销售季再投入5百万元广告费,则估计销售额约可达47.1百万元 | |
| B. | 已知统计数据中的平均销售额为41.4百万元,则平均广告费为4百万元 | |
| C. | 广告费用x和销售额y之间的相关系数不能确定正负,但其绝对值趋于1 | |
| D. | 5.7的含义是广告费用每增加1百万元,销售额大约增长5.7百万元左右 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (-∞,0] | C. | [1,+∞) | D. | (-∞,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com