
分析 (Ⅰ)利用直接法,求曲线C的轨迹方程;
(Ⅱ)由于直线与圆有两个不同的交点,故圆心到直线l的距离应小于圆的半径,即可求直线l斜率的取值范围;
(Ⅲ)若x1x2+y1y2=3,求出k,即可求|DE|.
解答 解:(Ⅰ)设点P坐标为(x,y)
由|PA|=2|PB|得:$\sqrt{(x+2)^{2}+{y}^{2}}$=2$\sqrt{(x-1)^{2}+{y}^{2}}$
整理得:曲线C的轨迹方程为(x-2)2+y2=4…(4分)
(II)依题意:设直线l的方程为:y=kx-3.
由于直线与圆有两个不同的交点,故圆心到直线l的距离应小于圆的半径,即:d=$\frac{|2k-3|}{\sqrt{1+{k}^{2}}}$<2,
∴$k>\frac{5}{12}$…(8分)
(Ⅲ)设直线l的方程为:y=kx-3.
代入(x-2)2+y2=4,整理得(1+k2)x2-(4+6k)x+9=0
∵直线l与圆C相交于不同两点D(x1,y1),E(x2,y2)
∴x1+x2=$\frac{4+6k}{1+{k}^{2}}$,x1x2=$\frac{9}{1+{k}^{2}}$,
y1y2=(kx1-3)(kx2-3)=$\frac{9-12k}{1+{k}^{2}}$
又∵x1x2+y1y2=3,
∴$\frac{9}{1+{k}^{2}}$+$\frac{9-12k}{1+{k}^{2}}$=3,
整理得:k2+4k-5=0,解得k=1或-5(舍)…(10分)
∴直线l的方程为:y=x-3,
圆心C到l的距离d=$\frac{\sqrt{2}}{2}$,|DE|=2$\sqrt{4-\frac{1}{2}}$=$\sqrt{14}$…(12分)
点评 本题考查轨迹方程,考查直线与圆的位置关系,考查韦达定理的运用,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知全集U=R,集合A={x|1≤x≤3},B={x|2<x<4}.
已知全集U=R,集合A={x|1≤x≤3},B={x|2<x<4}.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在(0,+∞)上有最小值 | B. | 函数f(x)在(0,+∞)上没有最大值 | ||
| C. | 函数f(x)在R上没有极小值 | D. | 函数f(x)在R上有极大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
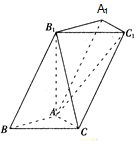 已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.
已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com