
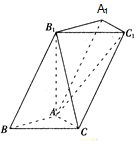
 已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.
已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.分析 (1)推导出AB1⊥AB.AC⊥AB.由此能证明AB⊥平面AB1C.
(2)多面体CAA1B1C1的体积:${V_{ABC-{A_1}{B_1}{C_1}}}-{V_{{B_1}-ABC}}=\frac{2}{3}{V_{ABC-{A_1}{B_1}{C_1}}}$.由此能求出结果.
解答 证明:(1)依题意,∠BAA1=120°,
故∠ABB1=60°,
在△ABB1中,AB=1,BB1=AA1=2,∠ABB1=60°,
由余弦定理得$A{B_1}^2=A{B^2}+B{B_1}^2-2AB•B{B_1}•cos∠AB{B_1}=3$,
∴$A{B_1}=\sqrt{3}$,∴$B{B_1}^2=A{B^2}+A{B_1}^2$,
∴AB1⊥AB.又∵∠BAC=90°,∴AC⊥AB.
又∵AC∩AB1=A,
∴AB⊥平面AB1C.
解:(2)∵$A{B_1}=\sqrt{3},AC=1,{B_1}C=2$,故AB1⊥AC,
∵AB1⊥AB,AC∩AB=A,故AB1⊥平面ABC,
依题意,多面体CAA1B1C1的体积:
${V_{ABC-{A_1}{B_1}{C_1}}}-{V_{{B_1}-ABC}}=\frac{2}{3}{V_{ABC-{A_1}{B_1}{C_1}}}=\frac{2}{3}×\sqrt{3}×\frac{1}{2}×1×1=\frac{{\sqrt{3}}}{3}$.
点评 本题考查线面垂直的证明,考查多面体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
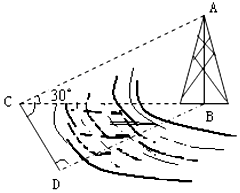 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{3}{2},5}]$ | B. | $[{\frac{2}{3},5}]$ | C. | $[{\frac{3}{2},7}]$ | D. | $[{\frac{2}{3},7}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“p或q”是假命题 | B. | 命题“p且q”是真命题 | ||
| C. | 命题“非q”是假命题 | D. | 命题“p且‘非q’”是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
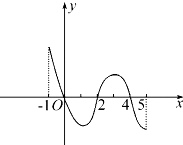 已知函数f(x)的定义域为[-1,5],部分对应值如表:
已知函数f(x)的定义域为[-1,5],部分对应值如表:| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 0 | 2 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com