
| A. | 命题“p或q”是假命题 | B. | 命题“p且q”是真命题 | ||
| C. | 命题“非q”是假命题 | D. | 命题“p且‘非q’”是真命题 |
分析 先判断命题p,q的真假,进而根据复合命题真假判断的真值表,可得答案.
解答 解:若方程$\frac{x^2}{m-5}-\frac{y^2}{m+3}=1$表示双曲线,
则(m-5)(m+3)>0,
解得:m<-3,或m>5;
故命题p是假命题,
sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$)∈[-$\sqrt{2}$,$\sqrt{2}$],
故命题命题q:存在x0∈R,使得sinx0-cosx0=2,是假命题,
故命题“p或q”,“p且q”,p且‘非q’”是假命题,
命题“非q”是真命题,
故选:A
点评 本题以命题的真假判断与应用为载体,考查了复合命题,充要条件,双曲线的方程,三角函数的值域,特称命题,难度中档.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6-4ln2}{ln2}$ | B. | $\frac{6}{ln2}+4$ | C. | $\frac{12}{ln2}-4$ | D. | 3e-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
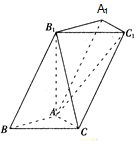 已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.
已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数g(x)与u(x)的值域相同 | B. | 函数g(x)与u(x)的最小正周期相同 | ||
| C. | 函数g(x)与u(x)的单调区间相同 | D. | 函数g(x)与u(x)奇偶性相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
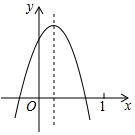 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程的两根之和大于0;④a-b+c<0,其中正确的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程的两根之和大于0;④a-b+c<0,其中正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com