
| A�� | ��$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$����$\overrightarrow a��\overrightarrow b$ | |
| B�� | ��a��b��cΪʵ������a��b��0����$\frac{b}{a}��\frac{a}{b}$ | |
| C�� | ��֪m��n�ǿռ�������ͬ��ֱ�ߣ������£����ǿռ�������ͬ��ƽ�棬�����ɦ�=m���¡ɦ�=n��m��n����Φ� | |
| D�� | ��ֱ֪��l1��A1x+B1y+C1=0��l2��A2x+B2y+C2=0����A1B2=A2B1����l1��l2 |
���� ����������ϵ�ж�A��������ʽ�Ļ��������ж�B�����ռ�ֱ����ƽ���λ�ù�ϵ�ж�C������ֱ����ֱ��ƽ�еij�Ҫ�����ж�D������
��� �⣺����A����$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$����������$\overrightarrow{a}$��$\overrightarrow{b}$���߷�����$\overrightarrow a��\overrightarrow b$��A����ȷ��
����B����a��b��cΪʵ������a��b��0���ɵ�a2��b2��$\frac{b}{a}��\frac{a}{b}$��������
����C����֪m��n�ǿռ�������ͬ��ֱ�ߣ������£����ǿռ�������ͬ��ƽ�棬�����ɦ�=m���¡ɦ�=n��m��n����Φ��п����ཻ������C����ȷ��
����D����ֱ֪��l1��A1x+B1y+C1=0��l2��A2x+B2y+C2=0����A1B2=A2B1����l1��l2��Ҳ�����غϣ�����D����ȷ��
��ѡ��B��
���� ���⿼���������ٵ��ж���Ӧ�ã��漰���������봹ֱ������ʽ�Ļ������ʣ��ռ�ֱ����ֱ�ߣ�ֱ����ƽ���λ�ù�ϵ��Ӧ�ã�


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ | B�� | ��Ҫ����� | ||
| C�� | ��Ҫ | D�� | �Ȳ����Ҳ����Ҫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �Ķ���ͼ�ij����ͼ��������Ӧ�ij���������N��ֵΪ17�������N��ֵΪ��������
�Ķ���ͼ�ij����ͼ��������Ӧ�ij���������N��ֵΪ17�������N��ֵΪ��������| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������ع�ϵ����������x��y֮��ļ����������±���ʾ��
��֪������ع�ϵ����������x��y֮��ļ����������±���ʾ��| x | 2 | 4 | 6 | 8 | 10 |
| y | 3 | 6 | 7 | 10 | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
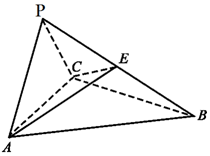 ��ͼ������P-ABC�У���ABC���������Σ���ACP��ֱ�������Σ���ABP=��CBP��AB=BP��
��ͼ������P-ABC�У���ABC���������Σ���ACP��ֱ�������Σ���ABP=��CBP��AB=BP���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com