
 已知具有相关关系的两个变量x,y之间的几组数据如下表所示:
已知具有相关关系的两个变量x,y之间的几组数据如下表所示:| x | 2 | 4 | 6 | 8 | 10 |
| y | 3 | 6 | 7 | 10 | 12 |
分析 (1)根据表中数据画出散点图即可;
(2)计算平均数与回归系数,写出回归直线方程,利用方程计算x=20时y的值;
(3)用列举法求出基本事件数,计算对应的概率值.
解答 解:(1)根据表中数据,画出散点图如图所示: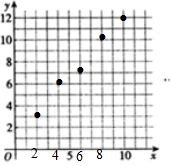
(2)依题意,计算$\overline x=\frac{1}{5}(2+4+6+8+10)=6$,
$\overline y=\frac{1}{5}(3+6+7+10+12)=7.6$,
$\sum_{i=1}^5{x_i^2}=4+16+36+64+100=220$,
$\sum_{i=1}^5{{x_i}{y_i}}=6+24+42+80+120=272$,
b=$\frac{{\sum_{i=1}^5{{x_i}{y_i}-5\overline x\overline y}}}{{\sum_{i=1}^5{x_i^2}-5{{(\overline x)}^2}}}$=$\frac{272-5×6×7.6}{{220-5×{6^2}}}$=$\frac{44}{40}$=1.1,
∴a=7.6-1.1×6=1$;
∴回归直线方程为y=1.1x+1,
当x=20时,y=1.1×20+1=23;
(3)五个点中落在直线2x-y-4=0右下方的三个点记为A,B,C,另外两个点记为d,e,
从这五个点中任取两个点的结果有
(A,B),(A,C),(A,d),(A,e),(B,C),
(B,d),(B,e),(C,d),(C,e),(d,e)共10个,
其中两个点均在直线2x-y-4=0的右下方的结果有3个,
所求的概率为$P=\frac{3}{10}$.
点评 本题考查了散点图与线性回归方程的计算问题,也考查了列举法求古典概型的概率问题,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,-3} | B. | {1,0} | C. | {1,3} | D. | {1,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$,则$\overrightarrow a⊥\overrightarrow b$ | |
| B. | 若a,b,c为实数,且a<b<0,则$\frac{b}{a}<\frac{a}{b}$ | |
| C. | 已知m,n是空间两条不同的直线,α,β,γ是空间三个不同的平面,若α∩γ=m,β∩γ=n,m∥n则α∥β | |
| D. | 已知直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,若A1B2=A2B1,则l1∥l2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\{α|α=2kπ-\frac{π}{3},k∈Z\}$ | B. | $\{α|α=2kπ+\frac{2π}{3},k∈Z\}$ | C. | $\{α|α=kπ-\frac{2π}{3},k∈Z\}$ | D. | $\{α|α=kπ-\frac{π}{3},k∈Z\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 4月1日 | 4月6日 | 4月12日 | 4月19日 | 4月27日 |
| 温差x/oC | 2 | 3 | 5 | 4 | 1 |
| 发芽数y/颗 | 9 | 11 | 15 | 13 | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com