
| A�� | �٢� | B�� | �ڢܢ� | C�� | �� | D�� | �� |
���� ���˸���Ӳ��һ�Σ����еĽ����8�֣����ڵ���һ�����õĽ�����������˲�ͬʱ�����˾ͳ�������Ϸ��ֹ���ٵ��м����õĽ�����������˲�ͬʱ������2�ֽ�����ڵ�һ�����˳���ʱ����6�ֽ���������ڵ����ֲ����˳��֣���ǰ�������˳��֣�������ֱ���ھžֲ����˳��֣���ǰ8�����˳��֣���ֱ���ھžֲ����˳��֣���������Ϸ����ֹǰ�������������֣���ǰ5�������˳������������Ӧ�ĸ��ʣ�
��� �⣺���˸���Ӳ��һ�Σ�ÿһ����Ӳ�Ҷ���2�ֽ�������еĽ������23=8�֣�
���ڵ���һ�����õĽ�����������˲�ͬʱ�����˾ͳ�������Ϸ��ֹ��
�ٵ��м����õĽ�����������˲�ͬʱ������������������������2�ֽ����
�ʵ�һ�ּͳ��ֵĸ�����$\frac{1}{4}$���ʢٴ���
�ڵ�һ�����˳���ʱ��������������������������������������������������������6�ֽ����
�ʵ�һ�����˳��ֵĸ�����$\frac{3}{4}$���ʢڴ���
�����ڵ����ֲ����˳��֣���ǰ�������˳��֣�
�ʵ����ֲ����˳��ֵĸ�����$\frac{2}{8}��\frac{2}{8}��\frac{6}{8}$=$\frac{3}{64}$���ʢ���ȷ��
������ֱ���ھžֲ����˳��֣���ǰ8�����˳��֣���ֱ���ھžֲ����˳��֣�
��׳��ֵĸ����ǣ�$\frac{2}{8}$��8��$\frac{6}{8}$��$\frac{1}{3}$=$\frac{1}{{4}^{9}}$���ʢܴ���
��������Ϸ����ֹǰ�������������֣���ǰ5�������˳���
�ʸ���Ϸ����ֹǰ�������������ֵĸ���Ϊ��
1-$\frac{6}{8}-\frac{2}{8}��\frac{6}{8}-��\frac{2}{8}��^{2}��\frac{6}{8}$-$��\frac{2}{8}��^{3}��\frac{6}{8}$-$��\frac{2}{8}��^{4}��\frac{6}{8}$=$\frac{1}{{4}^{5}}$���ʢݴ���
�ʴ�Ϊ���ۣ�
���� ���⿼��ŵ���ͼ�����ʼ��㹫ʽ��Ӧ�ã�����ѧ�������������������������е��⣮


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
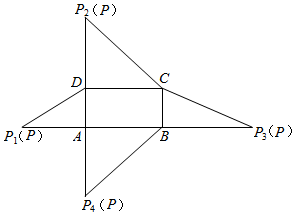
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 4�� | C�� | 6�� | D�� | 8�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
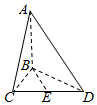 ��ͼ��������ABCD�У�AB��BC��CD��BD������ֱ��BC=BD=2����E��CD���е㣬����ֱ��AD��BE���ɽǵ�����ֵΪ$\frac{\sqrt{10}}{10}$����ֱ��BE��ƽ��ACD���ɽǵ�����ֵΪ��������
��ͼ��������ABCD�У�AB��BC��CD��BD������ֱ��BC=BD=2����E��CD���е㣬����ֱ��AD��BE���ɽǵ�����ֵΪ$\frac{\sqrt{10}}{10}$����ֱ��BE��ƽ��ACD���ɽǵ�����ֵΪ��������| A�� | $\frac{\sqrt{2}}{3}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{2\sqrt{2}}{3}$ | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
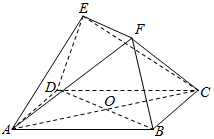 ��ͼ��������ABCDEF�У��ı���ABCD�DZ߳�Ϊ2�������Σ��ı���EFBDΪ�������Σ�EF��BD��EF=$\frac{1}{2}$BD��ƽ��EFBD��ƽ��ABCD��
��ͼ��������ABCDEF�У��ı���ABCD�DZ߳�Ϊ2�������Σ��ı���EFBDΪ�������Σ�EF��BD��EF=$\frac{1}{2}$BD��ƽ��EFBD��ƽ��ABCD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
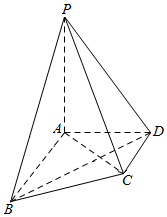 ������P-ABCD�У�AB��CD��AB��AD��PA=AB=2CD=4��$PB=2AD=4\sqrt{2}$��ƽ��PAB��ƽ��ABCD��
������P-ABCD�У�AB��CD��AB��AD��PA=AB=2CD=4��$PB=2AD=4\sqrt{2}$��ƽ��PAB��ƽ��ABCD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
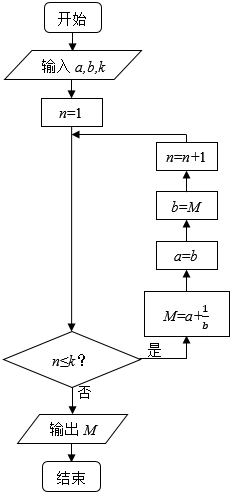 ִ����ͼ�ij����ͼ��������a��b��k�ֱ�Ϊ1��2��3���������M=��������
ִ����ͼ�ij����ͼ��������a��b��k�ֱ�Ϊ1��2��3���������M=��������| A�� | $\frac{2}{3}$ | B�� | $\frac{16}{5}$ | C�� | $\frac{7}{2}$ | D�� | $\frac{15}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com