“a＞4 是“方程x2+ax+a=0有两个负实数根的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件题目和参考答案——青夏教育精英家教网—

13．“a＞4”是“方程x²+ax+a=0有两个负实数根”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

分析方程x²+ax+a=0有两个负实数根，则$\left\{\begin{array}{l}{△={a}^{2}-4a≥0}\\{-a＜0}\\{a＞0}\end{array}\right.$，解出即可判断出结论．

解答解：方程x²+ax+a=0有两个负实数根，则$\left\{\begin{array}{l}{△={a}^{2}-4a≥0}\\{-a＜0}\\{a＞0}\end{array}\right.$，解得a≥4，
∴“a＞4”是“方程x²+ax+a=0有两个负实数根”的充分不必要条件．
故选：A．

点评本题考查了一元二次方程的实数根与判别式的关系、根与系数的关系、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

8．若二次函数ax²+bx+c=0的两个实数根为-2，3（a＜0），则ax²+bx+c＞0的解集为（　　）

A．

{x|x＜-2或x＞3}

B．

{x|x＜-3或x＞2}

C．

{x|-2＜x＜3}

D．

{x|-3＜x＜2}

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

4．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x，则此双曲线的离心率为（　　）

A．

$\sqrt{3}$

B．

$\sqrt{2}$

C．

$\frac{\sqrt{6}}{2}$

D．

$\frac{3}{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

1．若函数$f（x）={（\frac{1}{2}）^x}-2，g（x）=a（x-a+3）$同时满足以下两个条件：
①?x∈R，f（x）＜0或g（x）＜0；
②?x∈（-1，1），f（x）g（x）＜0．
则实数a的取值范围为（2，4）．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

8．在△ABC中，内角A，B，C的对边分别为a，b，c，已知b²-a²=ac．
（Ⅰ）若$cosB=\frac{1}{4}$，a=1，求△ABC的面积；
（Ⅱ）若$A=\frac{π}{6}$，求B．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

18．△ABC的内角A，B，C所对的边分别为a，b，c，已知4sin²$\frac{A+B}{2}-cos2C=\frac{7}{2}$．
（Ⅰ）求角C的大小；
（Ⅱ）若c=$\frac{{\sqrt{3}}}{2}$，求a-b的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．

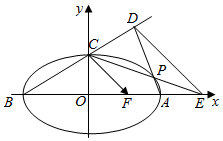如图：A，B，C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的顶点，点F（c，0）为椭圆的右焦点，原点O到直线CF的距离为$\frac{1}{2}c$，且椭圆过点$（{2\sqrt{3}，1}）$．
（Ⅰ）求椭圆的方程；
（Ⅱ）若P是椭圆上除顶点外的任意一点，直线CP交x轴于点E，直线BC与AP相交于点D，连结DE．设直线AP的斜率为k，直线DE的斜率为k₁，问是否存在实数λ，使得$λ{k_1}=k+\frac{1}{2}$成立，若存在求出λ的值，若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．