
 如图所示,抛物线C:y2=2px(p>0)的焦点为F,过点F且斜率存在的直线l交抛物线C于A,B两点,已知当直线l的斜率为1时,|AB|=8.
如图所示,抛物线C:y2=2px(p>0)的焦点为F,过点F且斜率存在的直线l交抛物线C于A,B两点,已知当直线l的斜率为1时,|AB|=8.分析 (Ⅰ)由题意设出直线l的方程,与抛物线方程联立,再由抛物线的焦点弦长公式列式求得p,则抛物线方程可求;
(Ⅱ)设出A的坐标,得到过A点的切线方程,与抛物线方程联立,利用判别式等于0把切线的斜率用A的纵坐标表示,进一步求得D点坐标,得到以AD为直径的圆的方程,从而得到存在定点M(1,0)在以AD为直径的圆上.
解答 解:(Ⅰ)由题意可得,直线l的方程为y=x-$\frac{p}{2}$,
联立方程$\left\{\begin{array}{l}{y=x-\frac{p}{2}}\\{{y}^{2}=2px}\end{array}\right.$,消去y整理得${x}^{2}-3px+\frac{{p}^{2}}{4}=0$,
设A(x1,y1),B(x2,y2),则x1+x2=3p,
故|AB|=x1+x2+p=4p=8,∴p=2,
∴抛物线C方程为y2=4x;
(Ⅱ)由(Ⅰ)知,直线x=-$\frac{p}{2}$即x=-1,A($\frac{{{y}_{1}}^{2}}{4},{y}_{1}$)(y1≠0),
设切线方程为$y-{y}_{1}=k(x-\frac{{{y}_{1}}^{2}}{4})$,
联立方程$\left\{\begin{array}{l}{y-{y}_{1}=k(x-\frac{{{y}_{1}}^{2}}{4})}\\{{y}^{2}=4x}\end{array}\right.$,消去x得:$\frac{k}{4}{y}^{2}-y+{y}_{1}-\frac{k{{y}_{1}}^{2}}{4}=0$,
∵△=$1-k({y}_{1}-\frac{k{{y}_{1}}^{2}}{4})=0$,∴$\frac{{k}^{2}{{y}_{1}}^{2}}{4}-k{y}_{1}+1=0$,即k=$\frac{2}{{y}_{1}}$,
∴切线方程为$y-{y}_{1}=\frac{2}{{y}_{1}}(x-\frac{{{y}_{1}}^{2}}{4})$,则4x-$2{y}_{1}y+{{y}_{1}}^{2}=0$,
令x=-1,得$y=\frac{{y}_{1}}{2}-\frac{2}{{y}_{1}}$,即D(-1,$\frac{{y}_{1}}{2}-\frac{2}{{y}_{1}}$),
∴以AD为直径的圆为$(x+1)(x-\frac{{{y}_{1}}^{2}}{4})+(y-{y}_{1})(y-\frac{{y}_{1}}{2}+\frac{2}{{y}_{1}})=0$,
由抛物线的对称性,若以AD为直径的圆经过定点,则此定点一定在x轴上,
∴令y=0,得$(x-1)(x+2-\frac{{{y}_{1}}^{2}}{4})=0$,得x=1,
故存在定点M(1,0)在以AD为直径的圆上.
点评 本题考查抛物线的简单性质,考查直线与圆、直线与抛物线位置关系的应用,考查计算能力,属中档题.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
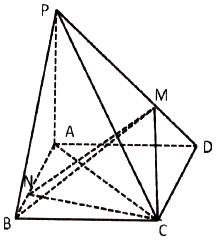 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,且PA=AB=AC=2,$BC=2\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,且PA=AB=AC=2,$BC=2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
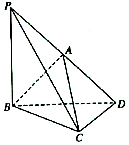 如图所示,在三棱锥A-BCD中,A在平面BCD内的投影恰为BD的中点,CD⊥BD,AD⊥AB,延长DA至P,使DA=AP.
如图所示,在三棱锥A-BCD中,A在平面BCD内的投影恰为BD的中点,CD⊥BD,AD⊥AB,延长DA至P,使DA=AP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线E:y2=2px(p>0)的焦点过为F,过F且倾斜角为$\frac{π}{4}$的直线l被E截得的线段长为8.
已知抛物线E:y2=2px(p>0)的焦点过为F,过F且倾斜角为$\frac{π}{4}$的直线l被E截得的线段长为8.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com