
分析 利用函数y=Asin(ωx+φ)的图象变换规律,诱导公式,得出结论.
解答 解:将y=$\sqrt{2}$sin(2x+$\frac{π}{3}$)的图象向右平移φ(0<φ<π)个单位得到y=$\sqrt{2}$sin(2x-2φ+$\frac{π}{3}$)的图象,
根据题意,得到函数y=2sinx(sinx-cosx)-1=2sin2x-sin2x-1=-sin2x-cos2x=-$\sqrt{2}$sin(2x+$\frac{π}{4}$)=$\sqrt{2}$sin(2x+$\frac{5π}{4}$)的图象,
∴-2φ+$\frac{π}{3}$=$\frac{5π}{4}$+2kπ,k∈Z,即 φ=-kπ-$\frac{11π}{24}$,∴φ=$\frac{13π}{24}$,
故答案为:$\frac{13π}{24}$.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,诱导公式的应用,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
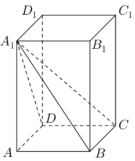 如图,长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=3;
如图,长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=3;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,抛物线C:y2=2px(p>0)的焦点为F,过点F且斜率存在的直线l交抛物线C于A,B两点,已知当直线l的斜率为1时,|AB|=8.
如图所示,抛物线C:y2=2px(p>0)的焦点为F,过点F且斜率存在的直线l交抛物线C于A,B两点,已知当直线l的斜率为1时,|AB|=8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
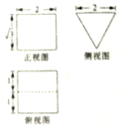
| A. | 20π | B. | $\frac{44}{3}$π | C. | $\frac{28}{3}$π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $2+\sqrt{2}$ | C. | $2+\sqrt{3}$ | D. | $3+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com