
分析 (Ⅰ)由题意圆心为M的动圆M过点(1,0),且与直线x=-1相切,利用抛物线的定义,可得圆心M的轨迹是以(1,0)为焦点的抛物线;圆心C在原点时,圆C的面积最小,可得圆C1的方程;
(Ⅱ)先求出b,再利用韦达定理,结合|AB|+|CD|=$\sqrt{1+\frac{1}{4}}$(x1-x3)+$\sqrt{1+\frac{1}{4}}$(x2-x4)=$\frac{\sqrt{5}}{2}$(x1+x2-x3-x4),可得结论.
解答 解:(I)∵动圆圆心到点F(1,0)的距离等于到定直线x=-1的距离,
∴动圆圆心的轨迹C为以F为焦点,以直线x=-1为准线的抛物线,
∴动圆圆心的轨迹方程为y2=4x.
圆心C在原点时,圆C的面积最小,此时圆C1的方程为x2+y2=1;
(II)F(1,9),设B(x1,y1),D(x2,y2),A(x3,y3),C(x4,y4),
由$\left\{\begin{array}{l}{y=\frac{1}{2}x+b}\\{{y}^{2}=4x}\end{array}\right.$,得x2+(4b-16)x+4b2=0,△>0,b<2,
x1+x2=16-4b,x1x2=4b2,
∵直线BF,DF的倾斜角互补,
∴kBF+kDF=0,
∵kBF+kDF=$\frac{{y}_{1}}{{x}_{1}-1}$+$\frac{{y}_{2}}{{x}_{2}-1}$,
∴y2(x1-1)+y1(x2-1)=0,
∴x1x2+(b-$\frac{1}{2}$)(x1+x2)-2b=0,
代入解得b=$\frac{1}{2}$,
由$\left\{\begin{array}{l}{y=\frac{1}{2}x+\frac{1}{2}}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,得5x2+2x-25=0,∴x3+x4=-$\frac{2}{5}$,
∴|AB|+|CD|=$\sqrt{1+\frac{1}{4}}$(x1-x3)+$\sqrt{1+\frac{1}{4}}$(x2-x4)=$\frac{\sqrt{5}}{2}$(x1+x2-x3-x4)=$\frac{36\sqrt{5}}{5}$.
点评 本题考查轨迹方程,考查直线与圆、直线与抛物线的位置关系,考查韦达定理的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
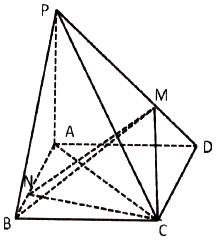 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,且PA=AB=AC=2,$BC=2\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,且PA=AB=AC=2,$BC=2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线E:y2=2px(p>0)的焦点过为F,过F且倾斜角为$\frac{π}{4}$的直线l被E截得的线段长为8.
已知抛物线E:y2=2px(p>0)的焦点过为F,过F且倾斜角为$\frac{π}{4}$的直线l被E截得的线段长为8.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{2}i$ | B. | $-\frac{5}{2}$ | C. | $-\frac{1}{2}i$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com