
分析 由条件利用二项式系数的性质求得n=4,再根据二项式展开式的通项公式求出第三项,可得第3项的系数.
解答 解:由于n为正偶数,且${({x^2}-\frac{1}{2x})^n}$的展开式中第3项的二项式系数最大,可得n=4,
故${({x^2}-\frac{1}{2x})^n}$=${{(x}^{2}-\frac{1}{2x})}^{4}$ 的展开式中第3项为 T3=${C}_{4}^{2}$•x4•${(-\frac{1}{2x})}^{2}$=$\frac{3}{2}$•x2,
故第3项的系数是$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
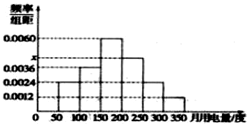 利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )
利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )| A. | 46 | B. | 48 | C. | 50 | D. | 52 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知斜四棱柱ABCD-A1B1C1D1的底面是矩形,侧面CC1D1D垂直底面ABCD,BC=2AB=DC1=2,BD1=2$\sqrt{3}$
已知斜四棱柱ABCD-A1B1C1D1的底面是矩形,侧面CC1D1D垂直底面ABCD,BC=2AB=DC1=2,BD1=2$\sqrt{3}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com