练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
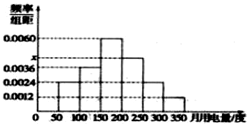
    1．利用简单随机抽样从某小区抽取100户居民进行月用电量调查，发现其用电量都在50到350度之间，频率分布直方图如图所示．在这些用户中，用电量落在区间[150，250]内的户数为（　　）
    A．46B．48C．50D．52

    分析 根据频率分布直方图，利用频率、频数与样本容量的关系进行解答即可．

    解答 解：这些用户中，用电量落在区间[150，250]内的频率为
    1-（0.0024+0.0036+0.0024+0.0012）×50=0.52
    ∴用电量落在区间[150，250]内的户数为
    100×0.52=52．
    故选：D．

    点评 本题考查了频率分布直方图的应用问题，也考查了频率=$\frac{频数}{样本容量}$的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．执行如图所示的程序，输出的S为（　　）
    A．-1006B．1007C．-1008D．1009

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在篮球比赛中，某篮球队队员投进三分球的个数如表所示：
    队员i123456
    三分球个数aia1a2a3a4a5a6
    如图是统计上述6名队员在比赛中投进的三分球总数s的程序
    框图，则图中的判断框内应填入的条件是（　　）
    A．i＜6B．i＜7C．i＜8D．i＜9

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设集合U={1，2，3，4}，A={1，2}，B={2，4}，则B∩（∁UA）=（　　）
    A．{2}B．{4}C．{1，2，4}D．{1，4}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．如图，在四棱锥P-ABCD中，PC⊥底面ABCD．底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2，AD=CD=1，E是线段PB的中点．
    （Ⅰ）证明：AC⊥平面PBC；
    （Ⅱ）若点P到平面ACE的距离是$\frac{{\sqrt{6}}}{3}$，求三棱锥P-ACD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．双曲线${y^2}-\frac{x^2}{m}=1$的离心率$e=\sqrt{3}$，则以双曲线的两条渐近线与抛物线y2=mx的交点为顶点的三角形的面积为（　　）
    A．$4\sqrt{2}$B．$12\sqrt{2}$C．$8\sqrt{2}$D．$16\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知n为正偶数，且${（{x^2}-\frac{1}{2x}）^n}$的展开式中第3项的二项式系数最大，则第3项的系数是$\frac{3}{2}$．（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．如图，在三棱锥S-ABC中，SA⊥底面ABC，AC=AB=SA=2，AC⊥AB，D，E分别是AC，BC的中点，F在SE上，且SF=2FE．
    （1）求证：AF⊥平面SBC；
    （2）在线段上DE上是否存在点G，使二面角G-AF-E的大小为30°？若存在，求出DG的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．圆x2+y2=4被直线$\sqrt{3}x+y-2\sqrt{3}$=0截得的弦长为（　　）
    A．$2\sqrt{3}$B．$2\sqrt{2}$C．3D．2

    查看答案和解析>>

    同步练习册答案