
 如图,在三棱锥S-ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D,E分别是AC,BC的中点,F在SE上,且SF=2FE.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D,E分别是AC,BC的中点,F在SE上,且SF=2FE.分析 (1)通过证明AF与平面SBC内的两条相交直线垂直即可;
(2)抓住两点找到问题的求解方向:一是点G的预设位置,二是二面角G-AF-E的位置,计算即可.
解答 (1)证明:由AC=AB=SA=2,AC⊥AB,E是BC的中点,得$AE=\sqrt{2}$.
因为SA⊥底面ABC,所以SA⊥AE.
在Rt△SAE中,$SE=\sqrt{6}$,所以$EF=\frac{1}{3}SE=\frac{{\sqrt{6}}}{3}$.
因此AE2=EF•SE,又因为∠AEF=∠AES,
所以△EFA∽△EAS,
则∠AFE=∠SAE=90°,即AF⊥SE.
因为SA⊥底面ABC,所以SA⊥BC,又BC⊥AE,
所以BC⊥底面SAE,则BC⊥AF.
又SE∩BC=E,所以AF⊥平面SBC.  (2)结论:在线段上DE上存在点G使二面角G-AF-E的大小为30°,此时DG=$\frac{1}{2}$.
(2)结论:在线段上DE上存在点G使二面角G-AF-E的大小为30°,此时DG=$\frac{1}{2}$.
理由如下:
假设满足条件的点G存在,并设DG=t.
过点G作GM⊥AE交AE于点M,
又由SA⊥GM,AE∩SA=A,得GM⊥平面SAE.
作MN⊥AF交AF于点N,连结NG,则AF⊥NG.
于是∠GNM为二面角G-AF-E的平面角,
即∠GNM=30°,由此可得$MG=\frac{{\sqrt{2}}}{2}(1-x)$.
由MN∥EF,得$\frac{MN}{EF}=\frac{AM}{AE}$,
于是有$\frac{MN}{{\frac{{\sqrt{6}}}{3}}}=\frac{{\frac{{\sqrt{2}}}{2}(1+t)}}{{\sqrt{2}}}$,$MN=\frac{{\sqrt{6}}}{6}(1+t)$.
在Rt△GMN中,MG=MNtan30°,
即$\frac{{\sqrt{2}}}{2}(1-t)=\frac{{\sqrt{6}}}{6}(1+t)•\frac{{\sqrt{3}}}{3}$,解得$t=\frac{1}{2}$.
于是满足条件的点G存在,且$DG=\frac{1}{2}$.
点评 本题考查空间几何图形中线面关系的平行或垂直的证明及空间角的计算,考查空间想象能力,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
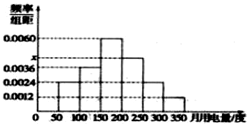 利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )
利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )| A. | 46 | B. | 48 | C. | 50 | D. | 52 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知斜四棱柱ABCD-A1B1C1D1的底面是矩形,侧面CC1D1D垂直底面ABCD,BC=2AB=DC1=2,BD1=2$\sqrt{3}$
已知斜四棱柱ABCD-A1B1C1D1的底面是矩形,侧面CC1D1D垂直底面ABCD,BC=2AB=DC1=2,BD1=2$\sqrt{3}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com