
| A. | $4\sqrt{2}$ | B. | $12\sqrt{2}$ | C. | $8\sqrt{2}$ | D. | $16\sqrt{2}$ |
分析 根据双曲线${y^2}-\frac{x^2}{m}=1$的离心率$e=\sqrt{3}$,求出m的值,可得双曲线的两条渐近线方程,抛物线方程,联立求出交点坐标,即可求出三角形的面积.
解答 解:∵双曲线${y^2}-\frac{x^2}{m}=1$的离心率$e=\sqrt{3}$,
∴$\frac{1+m}{1}$=3,
∴m=2,
∴双曲线的两条渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,抛物线方程为y2=2x,
联立可得交点坐标为(4,±2$\sqrt{2}$),
∴所求三角形的面积为$\frac{1}{2}×4×4\sqrt{2}$=8$\sqrt{2}$.
故选:C.
点评 本题考查双曲线的性质,考查双曲线与抛物线的位置关系,考查学生的计算能力,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
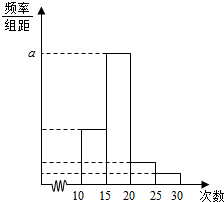 对某校高一年级学生参加“社区志愿者”活动次数进行统计,随机抽取M名学生作为样本,得到这M个学生参加“社区志愿者”活动的次数.据此作出频数和频率统计表及频率分布直方图如下:
对某校高一年级学生参加“社区志愿者”活动次数进行统计,随机抽取M名学生作为样本,得到这M个学生参加“社区志愿者”活动的次数.据此作出频数和频率统计表及频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 5 | 0.25 |
| [15,20) | 12 | n |
| [20,25) | m | p |
| [25,30] | 1 | 0.05 |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,-1) | B. | (-3,5] | C. | (3,5] | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
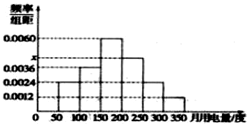 利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )
利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )| A. | 46 | B. | 48 | C. | 50 | D. | 52 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com