考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)利用递推关系式求出数列中的各项的值.
(2)利用递推关系式求数列的通项公式,先进行分类,进一步总结出数列的通项公式.
(3)根据(2)的结论,进一步求出数列{bn}的通项公式,再利用数学归纳法进行证明,从而得到恒成立问题.
解答:
(1)证明:各项均不为零的数列{a
n}的前n项和为S
n,且4S
n=a
n•a
n+1+1(n∈N
*),
其中a
1=1.
则:当n=1时,解得:a
2=3
当n=2时,解得:a
3=5
当n=3时,解得:a
4=7
当n=4时,解得:a
5=9
由于:2a
3=a
1+a
5所以:a
1,a
3,a
5成等差数列.
(2)证明:由于4S
n=a
na
n+1+1①
所以:4S
n-1=a
na
n-1+1②
①-②得:a
n+1-a
n-1=4
则数列的相邻项成等差数列.
③当数列是奇数项时,a
1=1公差为4
则:数列a
n=1+4(n-1)=4n-3
④当数列是偶数项时,a
2=3
则:数列a
n=3+4(n-1)=4n-1
则相邻项的差值为2,所以数列{a
n}为等差数列.
(3)解:由(2)得到:a
n=1+2(n-1)=2n-1
所以:
2bn=1+整理得:
bn=log2T
n=b
1+b
2+…+b
n=
log2(••…)则:要使不等式2T
n>log
2a
n+1恒成立
只需满足
2log2(•…)>log2an+1恒成立即可.
即:
••…>恒成立
用数学归纳法证明:
①当n=1时,2>
恒成立.
②当n=k时,
••…>恒成立
则:当n=k+1时,
(••…)>=
=
>>=
所以无论n取任意正整数上述不等式恒成立.
点评:本题考查的知识要点:利用递推关系式求数列的通项公式,数学归纳法的应用.属于中等题型.



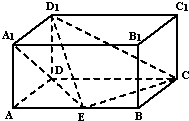 如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点
如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点