
【题目】已知![]() ,函数
,函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,且
,且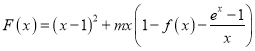 在
在![]() 时有极大值点
时有极大值点![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)对![]() 求导,分
求导,分![]() ,
,![]() ,
,![]() ,
,![]() 进行讨论,可得函数
进行讨论,可得函数![]() 的单调性;
的单调性;
(2)将![]() 代入
代入![]() ,对
,对![]() 求导,可得
求导,可得![]() ,再对
,再对![]() 求导,可得函数
求导,可得函数![]() 有唯一极大值点
有唯一极大值点![]() ,且
,且![]() .
.
可得![]() ,设
,设![]() ,对其求导后可得
,对其求导后可得![]() .
.
解:(1)![]() ,
,
又![]() ,
,![]() ,
,![]() 时,
时,![]() ,所以可解得:函数
,所以可解得:函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减;
单调递减;
经计算可得,![]() 时,函数
时,函数![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,
单调递增,![]() 单调递减;
单调递减;
![]() 时,函数
时,函数![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,
单调递增,![]() 单调递减;
单调递减;
![]() 时,函数
时,函数![]() 在
在![]() 单调递减.
单调递减.
综上:![]() 时,函数
时,函数![]() 在
在![]() 单调递增,
单调递增,![]() 单调递减;
单调递减;
![]() 时,函数
时,函数![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,
单调递增,![]() 单调递减;
单调递减;
![]() 时,函数
时,函数![]() 在
在![]() 单调递减;
单调递减;
![]() 时,函数
时,函数![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,
单调递增,![]() 单调递减.
单调递减.
(2)若![]() ,则
,则![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 单调递减,即
单调递减,即![]() 单调递减,
单调递减,
当![]() 时,
时,![]() 单调递增,即
单调递增,即![]() 单调递增.
单调递增.
又因为![]() 由
由![]() 可知:
可知:![]() ,
,
而![]() ,且
,且![]() ,
,
![]() ,使得
,使得![]() ,且
,且![]() 时,
时,![]() 单调递增,
单调递增,
![]() 时,
时,![]() 单调递减,
单调递减,![]() 时,
时,![]() 单调递增,
单调递增,
所以函数![]() 有唯一极大值点
有唯一极大值点![]() ,
,
且![]() .
.
![]()
![]() .
.
所以![]() ,
,
设![]() (
(![]() ),则
),则![]() ,
,
![]() 在
在![]() 单调递增,
单调递增,![]() ,
,![]() ,又因为
,又因为![]() ,
,
![]()
![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】已知点M(x,y)满足![]()
(1)求点M的轨迹E的方程;
(2)设过点N(﹣1,0)的直线l与曲线E交于A,B两点,若△OAB的面积为![]() (O为坐标原点).求直线l的方程.
(O为坐标原点).求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四名同学组成一个4![]() 100米接力队,老师要安排他们四人的出场顺序,以下是他们四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求,据此我们可以断定在老师安排的出场顺序中跑第三棒的人是_________.
100米接力队,老师要安排他们四人的出场顺序,以下是他们四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求,据此我们可以断定在老师安排的出场顺序中跑第三棒的人是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年5月31日晚,大连市某重点高中举行一年一度的毕业季灯光表演.学生会共安排6名高一学生到学校会议室遮挡4个窗户,要求两端两个窗户各安排1名学生,中间两个窗户各安排两名学生,不同的安排方案共有( )
A.720B.360C.270D.180
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为 (为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线
(为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若![]() 与
与![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国![]() 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米至75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从市区2016年全年每天的
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米至75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从市区2016年全年每天的![]() 监测数据中,随机抽取15天的数据作为样本,监测值如茎叶图所示:(十位为茎,个位为叶)
监测数据中,随机抽取15天的数据作为样本,监测值如茎叶图所示:(十位为茎,个位为叶)
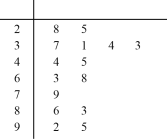
(1)从这15天的数据中任取3天的数据,求空气质量至少有一天达到一级的概率;
(2)以这15天的![]() 日均值来估算一年的空气质量情况,则一年(按360天计算)中大致有多少天的空气质量达到一级.
日均值来估算一年的空气质量情况,则一年(按360天计算)中大致有多少天的空气质量达到一级.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<![]() )的图象如图所示,为了得到g(x)=Acosωx的图象,只需把y=f(x)的图象上所有的点( )
)的图象如图所示,为了得到g(x)=Acosωx的图象,只需把y=f(x)的图象上所有的点( )

A. 向右平移![]() 个单位长度 B. 向左平移
个单位长度 B. 向左平移![]() 个单位长度
个单位长度
C. 向右平移![]() 个单位长度 D. 向左平移
个单位长度 D. 向左平移![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在观察物体时,从物体上、下沿引出的光线在人眼处所成的夹角叫视角.研究表明,视角在![]() 范围内视觉效果最佳.某大广场竖立的大屏幕,屏幕高为20米,屏幕底部距离地面11.5米.站在大屏幕正前方,距离屏幕所在平面
范围内视觉效果最佳.某大广场竖立的大屏幕,屏幕高为20米,屏幕底部距离地面11.5米.站在大屏幕正前方,距离屏幕所在平面![]() 米处的某人,眼睛位置距离地面高度为1.5米,观察屏幕的视角为
米处的某人,眼睛位置距离地面高度为1.5米,观察屏幕的视角为![]() (情景示意图如图所示).
(情景示意图如图所示).
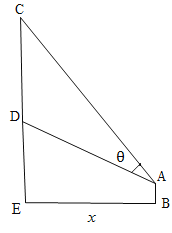
(1)为探究视觉效果,请从![]() ,
,![]() ,
,![]() 中选择一个作为
中选择一个作为![]() ,并求
,并求![]() 的表达式;
的表达式;
(2)根据(1)的选择探究![]() 是否有达到最佳视角效果的可能.
是否有达到最佳视角效果的可能.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com