Question

16．在平面直角坐标系xOy中，将函数y=$\sqrt{3+2x-{x}^{2}}$-$\sqrt{3}$（x∈[0，2]）的图象绕坐标原点O按逆时针方向旋转角θ，若?θ∈[0，a]，旋转后所得的曲线都是某个函数的图象，则a的最大值为60°．

Answer 1

分析 确定函数在x=0处，函数图象的切线斜率，可得倾斜角，从而可得结论．

解答 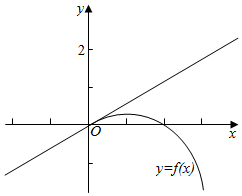解：由题意，函数图象如图所示，函数在[0，1]上为增函数，在[1，2]上为减函数．
设函数在x=0处，切线斜率为k，则k=f'（0）
∵f'（x）=$\frac{1}{2}$•$\frac{-2（x-1）}{\sqrt{3+2x-{x}^{2}}}$，
∴k=f'（0）=$\frac{\sqrt{3}}{3}$，可得切线的倾斜角为30°，
因此，要使旋转后的图象仍为一个函数的图象，旋转θ后的切线倾斜角最多为90°，也就是说，最大旋转角为90°-30°=60°，即θ的最大值为60°．
故答案为：60°

点评 本题考查了导数的几何意义和函数的图象与图象变化等知识点，将函数图象绕原点逆时针旋转θ后，所得曲线仍是一个函数的图象，求角θ的最大值，属于中档题．