
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
分析 根据三角函数的性质和角的范围进行判断.
解答 解:对于①,∵A-B∈(-π,π),B-C∈(-π,π),C-A∈(-π,π),
∴-1<cos(A-B)≤1,-1<cos(B-C)≤1,-1<cos(C-A)≤1.
∵cos(A-B)cos(B-C)cos(C-A)=1,∴cos(A-B)=cos(B-C)=cos(C-A)=1,
∴A-B=B-C=C-A=0,∴A=B=C,∴△ABC是等边三角形,故①正确.
对于②,若A=120°,B=30°,显然sinA=cosB,但△ABC不是直角三角形,故②错误.
对于③,若cosAcosBcosC<0,则cosA,cosB,cosC中必有一个小于0,即必有一个角为钝角,故③正确.
对于④,若sin2A=sin2B,则2A=2B,或2A+2B=π,∴A=B或A+B=$\frac{π}{2}$.
∴△ABC是等腰三角形或是直角三角形,故④错误.
故选:C.
点评 本题考查了三角函数的性质,解三角形,属于中档题.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:选择题
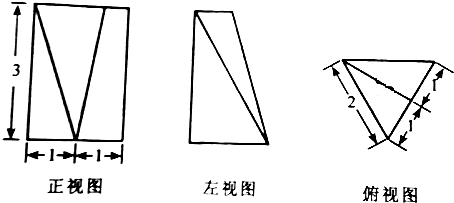
| A. | $\frac{3\sqrt{3}}{2}$ | B. | 2$\sqrt{3}$ | C. | $\frac{5\sqrt{3}}{2}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{20\sqrt{6}}{3}$ 米 | B. | 10$\sqrt{6}$ 米 | C. | $\frac{10\sqrt{6}}{3}$ 米 | D. | 20$\sqrt{2}$ 米 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3或$\frac{1}{3}$ | C. | $-\frac{1}{3}$ | D. | -3或$-\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)必为偶函数 | B. | f(x)必为奇函数 | ||
| C. | f(x)必为既奇又偶函数 | D. | 不能确定f(x)的奇偶性 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com