
 如图,四边形ABCD为矩形,四边形ABEF为等腰梯形,平面ABCD⊥平面ABEF,AB∥EF,AB=2AF,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.
如图,四边形ABCD为矩形,四边形ABEF为等腰梯形,平面ABCD⊥平面ABEF,AB∥EF,AB=2AF,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.分析 (1)通过证明CB⊥AB,推出CB⊥平面ABEF,得到CB⊥AF,利用余弦定理推出BF⊥AF,然后证明AF⊥平面CBF,得到平面ADF⊥平面CBF.
(2)取BF的中点Q,连接PO,PQ,OQ,说明PO∥AC,证明PO∥平面AFC,PQ∥平面AFC,推出平面POQ∥平面AFC,即可证明PM∥平面AFC.
解答 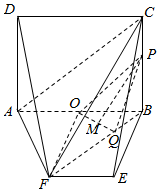 证明:(1)因为平面ABCD⊥平面ABEF,
证明:(1)因为平面ABCD⊥平面ABEF,
平面ABCD∩平面ABEF=AB,且CB⊥AB
所以CB⊥平面ABEF….(1分)
又AF?平面ABEF,所以CB⊥AF….(2分)
因为AB=2AF,∠BAF=60°,设AF=a,
由余弦定理得$BF=\sqrt{{a^2}+4{a^2}-2a×2acos{{60}^0}}=\sqrt{3}a$
所以AB2=AF2+BF2,即BF⊥AF…(4分)
又CB∩BF=B,所以AF⊥平面CBF….(5分)
又AF?平面ADF,
所以平面ADF⊥平面CBF…(6分)
(2)取BF的中点Q,连接PO,PQ,OQ…(7分)
因为P,O,Q分别是CB,AB,BF的中点,
所以PO∥AC,PO?平面AFC…(8分)
从而PO∥平面AFC,
同理PQ∥平面AFC…(9分)
又PO∩PQ=P,所以平面POQ∥平面AFC…(10分)
因为M为底面△OBF的重心,
所以M∈OQ,从而PM?平面POQ…(11分)
所以PM∥平面AFC.…(12分)
点评 本题考查直线与平面垂直,平面与平面垂直的判定定理的应用,直线与平面平行的判定定理的应用,考查空间想象能力以及计算能力.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0,1} | B. | {-2,-1,1,2} | C. | {-2,-1,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [{$\frac{1}{2}$,2] | B. | [$\frac{3-\sqrt{5}}{2}$,$\frac{3+\sqrt{5}}{2}$,] | C. | (0,$\frac{1}{2}$]∪[2,+∞) | D. | $({0,\frac{{3-\sqrt{5}}}{2}}]∪[{\frac{{3+\sqrt{5}}}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n+1-2 | B. | 3n | C. | 2n | D. | 3n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α∥β | B. | α⊥β | ||
| C. | α,β相交但不垂直 | D. | α,β所成的锐二面角为60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com