
分析 (1)利用三种方程的转化方法,求直线l和曲线C的极坐标方程;
(2)将直线l的参数方程代入椭圆C的普通方程,利用参数的几何意义,即可求|FA|•|FB|的最大值与最小值.
解答 解:(1)当α=$\frac{π}{4}$时,直线l:$\left\{\begin{array}{l}x=2+tcosα\\ y=tsinα\end{array}$的普通方程为x-y-2=0,极坐标方程为ρcosα-ρsinα-2=0;
椭圆C:$\left\{\begin{array}{l}x=3cosϕ\\ y=\sqrt{5}sinϕ\end{array}$(φ为参数)的普通方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}$=1,极坐标方程为5ρ2cos2α+9ρ2sin2α=45.(5分)
(2)将直线l的参数方程代入椭圆C的普通方程,并整理得:(5+4sin2α)t2+20tcosα-25=0.
设点A,B在直线参数方程中对应的参数分别为t1,t2,则
|FA|•|FB|=|t1t2|=$\frac{25}{5+4si{n}^{2}α}$.
当sinα=0时,|FA|•|FB|取最大值5;
当sinα=±1时,|FA|•|FB|取最小值$\frac{25}{9}$.…(5分)
点评 本题考查参数方程化成普通方程,考查学生的计算能力,正确运用参数的几何意义是关键.


科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{a_3}})$ | B. | $({0,\frac{2}{a_3}})$ | C. | $({0,\frac{1}{a_1}})$ | D. | $({0,\frac{2}{a_1}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
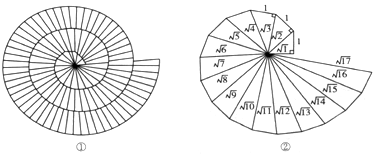
| A. | 120° | B. | 130° | C. | 135° | D. | 140° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (-1,2) | C. | (-∞,-1]∪[2,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
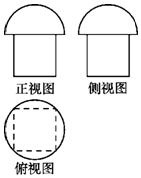 一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )| A. | $4+\frac{2π}{3}$ | B. | $4+\frac{{2\sqrt{2}π}}{3}$ | C. | $8+\frac{{4\sqrt{2}π}}{3}$ | D. | $8+\frac{{8\sqrt{2}π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (-∞,-1] | C. | (0,1] | D. | (-1,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com