
| A. | AB边中线的中点 | B. | AB边中线的三等分点(非重心) | ||
| C. | 重心 | D. | AB边的中点 |
分析 根据O是三角形的重心,得到三条中线上对应的向量的模长之间的关系,根据向量加法的平行四边形法则,求出向量的和,根据共线的向量的加减,得到结果.
解答 解:设AB 的中点是E,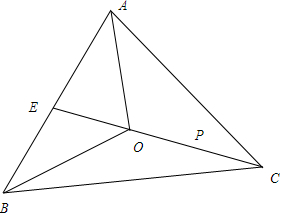
∵O是三角形ABC的重心,动点P满足$\overrightarrow{OP}$=$\frac{1}{3}$($\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OB}$+2$\overrightarrow{OC}$),
∴$\overrightarrow{OP}$=$\frac{1}{3}$($\overrightarrow{OE}$+2$\overrightarrow{OC}$)
∵$\overrightarrow{OC}$=2$\overrightarrow{EO}$,
∴$\overrightarrow{OP}$=$\frac{1}{3}$($\overrightarrow{OE}+4\overrightarrow{EO}$)=$\frac{1}{3}×3\overrightarrow{EO}$=$\overrightarrow{EO}$,
∴P在AB边的中线上,是中线的三等分点,不是重心.
故选:B.
点评 本题考查三角形的重心,考查向量加法的平行四边形法则,考查故选向量的加减运算,是一个比较简单的综合题目,这种题目可以以选择或填空出现.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
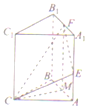 在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上
在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 生二胎 | 不生二胎 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 92 | 81 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | 5 | 2 | 7 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com