
| 1 |
| 3! |
| 1 |
| 5! |
| 1 |
| 7! |
| 1 |
| 3! |
| 1 |
| 5! |
| 1 |
| 7! |
| 1 |
| 2! |
| 1 |
| 4! |
| 1 |
| 6! |
| 1 |
| 8! |
| 1 |
| 3! |
| 1 |
| 5! |
| 1 |
| 7! |
| 1 |
| 2! |
| 1 |
| 4! |
| 1 |
| 6! |
| 1 |
| 8! |
| 1 |
| 8! |
| 1 |
| 8! |
| 1 |
| 2! |
| 1 |
| 4! |
| 1 |
| 6! |
| 1 |
| 8! |


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
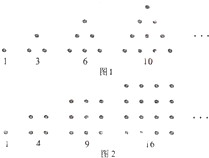 古希腊人常用小石子在沙滩上摆成各种形状研究数,如他们研究过图1中的1,3,6,10,…,由于这些数能表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数为正方形数,则除1外,最小的既是三角形数又是正方形数的是
古希腊人常用小石子在沙滩上摆成各种形状研究数,如他们研究过图1中的1,3,6,10,…,由于这些数能表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数为正方形数,则除1外,最小的既是三角形数又是正方形数的是查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 2 | 5 | 3 | 1 | 4 |
| f(x) | 1 | 2 | 3 | 4 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com