
分析 作出直观图,则十面体的体积为四棱锥的体积减去5个小棱锥的体积.根据相似比及三角形的面积公式得出小棱锥的体积.使用作差法求出十面体的体积.
解答 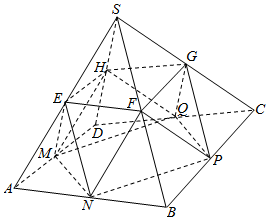 解:设四棱锥S-ABCD的底面积为S,高为h,则V=$\frac{1}{3}Sh$.
解:设四棱锥S-ABCD的底面积为S,高为h,则V=$\frac{1}{3}Sh$.
∴S四边形EFGH=$\frac{1}{4}S$,
∴S△AMN+S△CPQ=$\frac{1}{4}S$,S△BPN+S△DMQ=$\frac{1}{4}S$,
∴V棱锥S-EFGH=$\frac{1}{3}$•S四边形EFGH$•\frac{1}{2}h$=$\frac{1}{3}×\frac{S}{4}×\frac{h}{2}=\frac{V}{8}$.
V棱锥E-AMN+V棱锥G-CPQ=$\frac{1}{3}•$(S△AMN+S△CPQ)$•\frac{1}{2}h$=$\frac{V}{8}$,
V棱锥H-DMQ+V棱锥F-BNP=$\frac{1}{3}•$(S△BPN+S△DMQ)$•\frac{1}{2}h$=$\frac{V}{8}$.
∴十面体的体积为V-V棱锥S-EFGH-V棱锥E-AMN-V棱锥G-CPQ-V棱锥H-DMQ-V棱锥F-BNP=$\frac{5V}{8}$.
故答案为:$\frac{5V}{8}$.
点评 本题考查了棱锥的结构特征,棱锥的体积计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [1,2] | C. | [1,+∞) | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
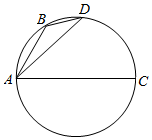 如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )| A. | 1 | B. | 2 | C. | t | D. | 2t |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 10 | C. | 32 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com