
分析 由条件利用三角函数的奇偶性、单调性、以及它们的图象的对称性,得出结论.
解答 解:①函数y=tanx在第一象限是增函数,错误,例如A=60°和B=420°,显然B>A,且它们都是第一象限角,但tanA=tanB.
②由于函数y=cos2($\frac{π}{4}$-x)=sinx是奇函数,故②错误;
③令x=$\frac{π}{6}$,求得y=0,可得函数y=sin(2x-$\frac{π}{3}$)的一个对称中心是($\frac{π}{6}$,0),故③正确;
④函数y=sin(x+$\frac{π}{4}$)在闭区间[-$\frac{π}{2}$,$\frac{π}{2}$]上,x+$\frac{π}{4}$∈[-$\frac{π}{4}$ $\frac{3π}{4}$],
故函数y=sin(x+$\frac{π}{4}$)在闭区间[-$\frac{π}{2}$,$\frac{π}{2}$]上不是增函数,故④错误,
故答案为:③.
点评 本题主要考查三角函数的奇偶性、单调性、以及它们的图象的对称性,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
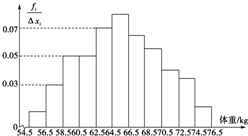 为了了解某地区高二学生的身体发育情况,抽查了该地区100名年龄为16.5岁~18岁的男生体重(kg),得到频率分布直方图如图所示.根据此图可得这100名学生中体重在[56.5,64.5)内的学生人数是( )
为了了解某地区高二学生的身体发育情况,抽查了该地区100名年龄为16.5岁~18岁的男生体重(kg),得到频率分布直方图如图所示.根据此图可得这100名学生中体重在[56.5,64.5)内的学生人数是( )| A. | 2 | B. | 30 | C. | 40 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com