Question

4．如图，在四边形ABCD中，AB=CD=1，BC=$\sqrt{3}$，且∠B=90°，∠BCD=120°，记向量$\overrightarrow{AB}=\overrightarrow{a}$，$\overrightarrow{AC}=\overrightarrow{b}$，则$\overrightarrow{AD}$=（　　）

• A． $\frac{2\sqrt{3}}{3}\overrightarrow{a}$-（1+$\frac{\sqrt{3}}{6}$）$\overrightarrow{b}$
• B． -$\frac{2\sqrt{3}}{3}\overrightarrow{a}$+（1+$\frac{\sqrt{3}}{6}$）$\overrightarrow{b}$
• C． -$\frac{2\sqrt{3}}{3}\overrightarrow{a}$+（1-$\frac{\sqrt{3}}{6}$）$\overrightarrow{b}$
• D． $\frac{2\sqrt{3}}{3}\overrightarrow{a}$+（1+$\frac{\sqrt{3}}{6}$）$\overrightarrow{b}$

Answer 1

分析 作DE⊥AB于E，CF⊥DE于F，转化$\overrightarrow{AD}=\overrightarrow{AE}+\overrightarrow{ED}$，求解即可．

解答 解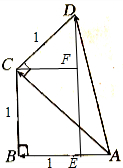：作DE⊥AB于E，CF⊥DE于F，
AB=CD=1，BC=$\sqrt{3}$，且∠B=90°，∠BCD=120°，记向量$\overrightarrow{AB}=\overrightarrow{a}$，$\overrightarrow{AC}=\overrightarrow{b}$，
所以$\overrightarrow{EF}=\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$=$\overrightarrow{b}-\overrightarrow{a}$，CF=BE=CD×cos30°=$\frac{\sqrt{3}}{2}$，DF=$\frac{1}{2}$，所以$\overrightarrow{DE}=（1+\frac{\sqrt{3}}{6}）\overrightarrow{BC}$，
则$\overrightarrow{AD}$=$\overrightarrow{AE}+\overrightarrow{ED}$=（1-$\frac{\sqrt{3}}{2}$）$\overrightarrow{a}$+（1+$\frac{\sqrt{3}}{6}$）$\overrightarrow{BC}$=（1-$\frac{\sqrt{3}}{2}$）$\overrightarrow{a}$+（1+$\frac{\sqrt{3}}{6}$）（$\overrightarrow{b}-\overrightarrow{a}$）=$-\frac{2\sqrt{3}}{3}\overrightarrow{a}+（1+\frac{\sqrt{3}}{6}）\overrightarrow{b}$；
故选B．

点评 本题考查向量在几何中的应用，准确利用已知条件是解题的关键．