Question

14．在平面直角坐标系xOy中，若动点P（a，b）到直线l₁：y=x，l₂：y=-x+1的距离分别为d₁，d₂，且满足d₁+2d₂=2$\sqrt{2}$，则a²+b²的最大值为$\frac{17}{2}$．

Answer 1

分析 利用点到直线的距离公式可得：|a-b|+2|a+b-1|=4．通过分类讨论可知：点（a，b）是如图所示的四边形的4条边．即可得到$\sqrt{{a}^{2}+{b}^{2}}$最大值．

解答 解：∵动点P（a，b）到两直线l₁：y=x和l₂：y=-x+的距离为d₁，d₂，且满足d₁+2d₂=2$\sqrt{2}$，
∴$\frac{|a-b|}{\sqrt{2}}$+2×$\frac{|a+b-1|}{\sqrt{2}}$=2$\sqrt{2}$，
化为|a-b|+2|a+b-1|=4．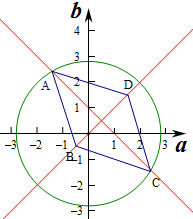
分为以下4种情况：
①$\left\{\begin{array}{l}{a-b≥0}\\{a+b-1≥0}\\{3a+b-6=0}\end{array}\right.$
②$\left\{\begin{array}{l}{a-b≥0}\\{a+b-1＜0}\\{a+3b+2=0}\end{array}\right.$，
③$\left\{\begin{array}{l}{a-b＜0}\\{a+b-1≥0}\\{a+3b-6=0}\end{array}\right.$，
④$\left\{\begin{array}{l}{a-b＜0}\\{a+b-1＜0}\\{3a+b+2=0}\end{array}\right.$．
可知点（a，b）是如图所示的四边形的4条边．
可知：当取点A或C时，$\sqrt{{a}^{2}+{b}^{2}}$取得最大值，
由$\left\{\begin{array}{l}{3a+b-6=0}\\{a+b-1=0}\end{array}\right.$得$\left\{\begin{array}{l}{a=\frac{5}{2}}\\{b=-\frac{3}{2}}\end{array}\right.$，
即C（$\frac{5}{2}$，-$\frac{3}{2}$），
此时a²+b²=（$\frac{5}{2}$）²+（-$\frac{3}{2}$）²=$\frac{25}{4}+\frac{9}{4}=\frac{34}{4}$=$\frac{17}{2}$．
故答案为：$\frac{17}{2}$

点评 本题考查了点到直线的距离公式、含绝对值的等式、分类讨论等基础知识与基本技能方法，难度较大．