练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    把下面在平面内成立的结论类比地推广到空间，并判断类比的结论是否成立：

    (1)如果一条直线和两条平行线中的一条相交，则必和另一条相交；

    (2)如果两条直线同时垂直于第三条直线，则这两条直线互相平行．


    解　(1)类比为：如果一个平面和两个平行平面中的一个相交，

    则必和另一个相交．

    结论是正确的：证明如下：设α∥β，且γ∩α＝a，

    则必有γ∩β＝b，若γ与β不相交，则必有γ∥β，

    又α∥β，∴α∥γ，与γ∩α＝a矛盾，∴必有γ∩β＝b.

    (2)类比为：如果两个平面同时垂直于第三个平面，则这两个平面互相平行，结论是错误的，这两个平面也可能相交．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    数列－3,7，－11,15，…的通项公式是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设M是具有以下性质的函数f(x)的全体：对于任意s>0，t>0，都有f(s)＋f(t)<f(s＋t)．给出函数f1(x)＝log2x，f2(x)＝2x－1.下列判断正确的是________．

    ①f1(x)∈M；②f1(x)∉M；

    ③f2(x)∈M；④f2(x)∉M.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    由1＝12,1＋3＝22,1＋3＋5＝32,1＋3＋5＋7＝42，…，得到1＋3＋…＋(2n－1)＝n2用的是________推理．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列{an}满足a1＝，an＋1＝1－，则a2 013＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    平面几何中圆的垂径定理(弦的中点与圆心的连线必定垂直于这条弦)，在解析几何中可以这样叙述：若M是圆O：x2＋y2＝r2(r>0)的弦AB的中点，则直线OM与AB的斜率之积为定值(即为－1)．

    (1)请在椭圆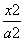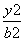＋＝1(a>b>0)中，写出与上述定理类似的结论，并予以证明．

    (2)若把(1)中的结论类比到双曲线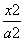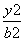－＝1(a>0，b>0)中，则直线OM与AB的斜率之积是什么？(不必证明)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a＝，b＝－，c＝－，则a，b，c的大小关系为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设A、B为两个集合，下列四个命题：

    ①A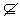B⇔对任意x∈A，有x∉B；②A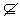B⇔A∩B＝∅；③A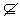B⇔A⊉B；④A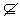B⇔存在x∈A，使得x∉B.

    其中真命题的序号是________(把符合要求的命题的序号都填上)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若直线mx－ny＝4与⊙O：x2＋y2＝4没有交点，则过点P(m，n)的直线与椭圆＋＝1的交点个数是________．

    查看答案和解析>>

    同步练习册答案