练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若直线mx－ny＝4与⊙O：x2＋y2＝4没有交点，则过点P(m，n)的直线与椭圆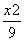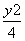＋＝1的交点个数是________．


    2

    解析　由题意>2，即m2＋n2<4，点(m，n)在以原点为圆心，2为半径的圆内，与椭圆＋＝1的交点个数为2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    把下面在平面内成立的结论类比地推广到空间，并判断类比的结论是否成立：

    (1)如果一条直线和两条平行线中的一条相交，则必和另一条相交；

    (2)如果两条直线同时垂直于第三条直线，则这两条直线互相平行．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b是实数，则“a>0且b>0”是“a＋b>0且ab>0”的________条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    判断下列命题的真假．

    (1)若x∈A∪B，则x∈B的逆命题与逆否命题；

    (2)若0<x<5，则|x－2|<3的否命题与逆否命题；

    (3)设a、b为非零向量，如果a⊥b，则a·b＝0的逆命题和否命题．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆的离心率为，焦点是(－3,0)，(3,0)，则椭圆方程为______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    点P(8,1)平分双曲线x2－4y2＝4的一条弦，则这条弦所在直线的方程是______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点P(3,4)是椭圆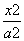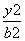＋＝1 (a>b>0)上的一点，F1、F2为椭圆的两焦点，若PF1⊥PF2，试求：

    (1)椭圆的方程；

    (2)△PF1F2的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知双曲线与椭圆＋＝1共焦点，它们的离心率之和为，求双曲线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列推理过程是演绎推理的是                                          

    A．由平面三角形的性质推测空间三棱锥的性质

    B．某校高二1班有55人，2班有52人，由此得高二所有班人数都超过50人

    C．两条直线平行，同位角相等；若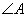与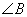是两条平行直线的同位角，则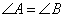

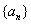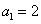    D．在数列中，，，由此归纳出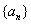的通项公式

    查看答案和解析>>

    同步练习册答案