
分析 根据题意可得F(-1,0),∠FAO=30°,OA=$\frac{OF}{tan∠FAO}$=1,由此求得OA的值,可得圆心C的坐标以及圆的半径,从而求得圆C方程.
解答 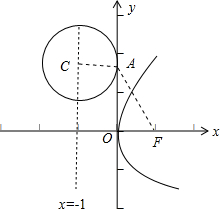 解:设抛物线y2=4x的焦点为F(1,0),准线l:x=-1,∵点C在l上,以C为圆心的圆与y轴的正半轴相切与点A,
解:设抛物线y2=4x的焦点为F(1,0),准线l:x=-1,∵点C在l上,以C为圆心的圆与y轴的正半轴相切与点A,
∵∠FAC=120°,∴∠FAO=30°,∴OA=$\frac{OF}{tan∠FAO}$=$\frac{1}{\frac{\sqrt{3}}{3}}$=1,∴OA=$\sqrt{3}$,∴A(0,$\sqrt{3}$),如图所示:
∴C(-1,$\sqrt{3}$),圆的半径为CA=1,故要求的圆的标准方程为 ${(x+1)^2}+{(y-\sqrt{3})^2}=1$,
故答案为:(x+1)2+${(y-\sqrt{3})}^{2}$=1.
点评 本题主要考查求圆的标准方程的方法,抛物线的简单几何性质,属于中档题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
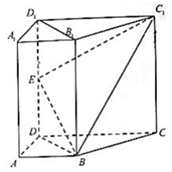 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overline{x}$=μ | B. | $\overline{x}$≈μ | C. | μ是$\overline{x}$的估计值 | D. | $\overline{x}$是μ的估计值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
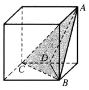 如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )
如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )| A. | 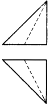 | B. | 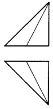 | C. | 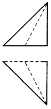 | D. | 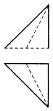 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com