
分析 一个大小方向确定的力分解为两个等大的力时,合力在分力的角平分线上,且两分力的夹角越大,分力越大,因而当绳子拉力达到F=10N的时候,绳子间的张角最大,为120°,此时两个挂钉间的距离最大.
解答 解:一个大小方向确定的力分解为两个等大的力时,合力在分力的角平分线上,且两分力的夹角越大,分力越大,
因而当绳子拉力达到F=10N的时候,绳子间的张角最大,为120°,此时两个挂钉间的距离最大;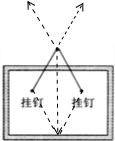
画框受到重力和绳子的拉力,三个力为共点力,受力如图.
绳子与竖直方向的夹角为θ=60°,绳子长为L=1m,则有mg=2Fcosθ,两个挂钉的间距离L=2×$\frac{L}{2}sinθ$,解得L=$\frac{\sqrt{3}}{2}$m,
故答案为:$\frac{\sqrt{3}}{2}$m.
点评 本题考查了力的合成与分解转化为向量的平行四边形法则,考查了推理能力与计算能力,属于中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
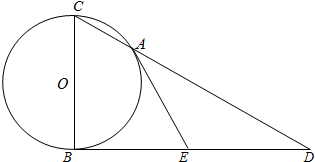 如图,过⊙O外一点E作⊙O的两条切线EA、EB,其中A、B为切点,BC为⊙O的一条直径,连CA并延长交BE的延长线于D点.
如图,过⊙O外一点E作⊙O的两条切线EA、EB,其中A、B为切点,BC为⊙O的一条直径,连CA并延长交BE的延长线于D点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
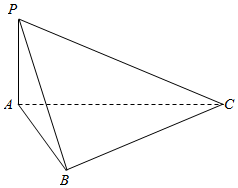 如图,在三棱锥P-ABC中,已知PA⊥平面ABC,平面PAB⊥平面PBC
如图,在三棱锥P-ABC中,已知PA⊥平面ABC,平面PAB⊥平面PBC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
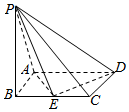 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,E为BC的中点,AB=1,AD=2,PA=2.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,E为BC的中点,AB=1,AD=2,PA=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{9}+\frac{y^2}{16}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | $1+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x<3x | B. | $\frac{1}{{{x^2}-x+1}}$>$\frac{1}{{{x^2}+x+1}}$ | ||
| C. | $\frac{1}{{{x^2}+1}}$>$\frac{1}{{{x^2}+2}}$ | D. | 2|x|<x2+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com